题目内容
19.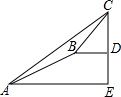 某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,那么大树CD的高度约为(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)( )
某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,那么大树CD的高度约为(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)( )| A. | 8.1米 | B. | 17.2米 | C. | 19.7米 | D. | 25.5米 |
分析 作BF⊥AE于F,则FE=BD=6米,DE=BF,设BF=x米,则AF=2.4米,在Rt△ABF中,由勾股定理得出方程,解方程求出DE=BF=5米,AF=12米,得出AE的长度,在Rt△ACE中,由三角函数求出CE,即可得出结果.
解答  解:作BF⊥AE于F,如图所示:
解:作BF⊥AE于F,如图所示:
则FE=BD=6米,DE=BF,
∵斜面AB的坡度i=1:2.4,
∴AF=2.4BF,
设BF=x米,则AF=2.4x米,
在Rt△ABF中,由勾股定理得:x2+(2.4x)2=132,
解得:x=5,
∴DE=BF=5米,AF=12米,
∴AE=AF+FE=18米,
在Rt△ACE中,CE=AE•tan36°=18×0.73=13.14米,
∴CD=CE-DE=13.14米-5米≈8.1米;
故选:A.
点评 本题考查了解直角三角形的应用、勾股定理、三角函数;由勾股定理得出方程是解决问题的关键.

练习册系列答案
相关题目
10.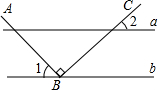 如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,那么∠2的度数是( )
如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,那么∠2的度数是( )
 如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,那么∠2的度数是( )
如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,那么∠2的度数是( )| A. | 20° | B. | 30° | C. | 35° | D. | 50° |
14. 如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=80°,则∠1等于( )
如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=80°,则∠1等于( )
 如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=80°,则∠1等于( )
如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=80°,则∠1等于( )| A. | 120° | B. | 110° | C. | 100° | D. | 80° |
11.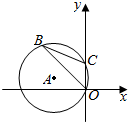 如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
 如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )| A. | $\frac{1}{3}$ | B. | 2$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{2\sqrt{2}}{3}$ |
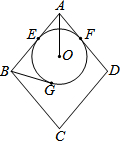 如图,菱形ABCD的边长为10,圆O分别与AB、AD相切于E、F两点,且与BG相切于G点.若AO=5,且圆O的半径为3,则BG的长度为何?( )
如图,菱形ABCD的边长为10,圆O分别与AB、AD相切于E、F两点,且与BG相切于G点.若AO=5,且圆O的半径为3,则BG的长度为何?( )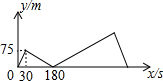 甲、乙两人在直线道路上同起点、同终点、同方向,分别以不同的速度匀速跑步1500米,先到终点的人原地休息,已知甲先出发30秒后,乙才出发,在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示,则乙到终点时,甲距终点的距离是175米.
甲、乙两人在直线道路上同起点、同终点、同方向,分别以不同的速度匀速跑步1500米,先到终点的人原地休息,已知甲先出发30秒后,乙才出发,在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示,则乙到终点时,甲距终点的距离是175米. =__________(a<0)
=__________(a<0)