题目内容
18.观察下列一组图形,其中图形①中共有2颗星,图形②中共有6颗星,图形③中共有11颗星,图形④中共有17颗星,…,按此规律,图形⑧中星星的颗数是( )
| A. | 43 | B. | 45 | C. | 51 | D. | 53 |
分析 设图形n中星星的颗数是an(n为正整数),列出部分图形中星星的个数,根据数据的变化找出变化规律“an=$\frac{1}{2}{n}^{2}$+$\frac{5}{2}$n-1”,依此规律即可得出结论.
解答 解:设图形n中星星的颗数是an(n为正整数),
∵a1=2=1+1,a2=6=(1+2)+3,a3=11=(1+2+3)+5,a4=17=(1+2+3+4)+7,
∴an=1+2+…+n+(2n-1)=$\frac{n(n+1)}{2}$+(2n-1)=$\frac{1}{2}{n}^{2}$+$\frac{5}{2}$n-1,
∴a8=$\frac{1}{2}$×82+$\frac{5}{2}$×8-1=51.
故选C.
点评 本题考查了规律型中的图形的变化类,根据图形中数的变化找出变化规律是解题的关键.

练习册系列答案
相关题目
6.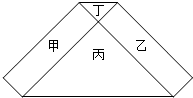 如图的六边形是由甲、乙两个长方形和丙、丁两个等腰直角三角形所组成,其中甲、乙的面积和等于丙、丁的面积和.若丙的一股长为2,且丁的面积比丙的面积小,则丁的一股长为何?( )
如图的六边形是由甲、乙两个长方形和丙、丁两个等腰直角三角形所组成,其中甲、乙的面积和等于丙、丁的面积和.若丙的一股长为2,且丁的面积比丙的面积小,则丁的一股长为何?( )
 如图的六边形是由甲、乙两个长方形和丙、丁两个等腰直角三角形所组成,其中甲、乙的面积和等于丙、丁的面积和.若丙的一股长为2,且丁的面积比丙的面积小,则丁的一股长为何?( )
如图的六边形是由甲、乙两个长方形和丙、丁两个等腰直角三角形所组成,其中甲、乙的面积和等于丙、丁的面积和.若丙的一股长为2,且丁的面积比丙的面积小,则丁的一股长为何?( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | 2-$\sqrt{3}$ | D. | 4-2$\sqrt{3}$ |
13. 如图,直线a,b被直线c所截,且a∥b,若∠1=55°,则∠2等于( )
如图,直线a,b被直线c所截,且a∥b,若∠1=55°,则∠2等于( )
 如图,直线a,b被直线c所截,且a∥b,若∠1=55°,则∠2等于( )
如图,直线a,b被直线c所截,且a∥b,若∠1=55°,则∠2等于( )| A. | 35° | B. | 45° | C. | 55° | D. | 125° |
10.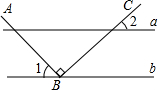 如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,那么∠2的度数是( )
如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,那么∠2的度数是( )
 如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,那么∠2的度数是( )
如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,那么∠2的度数是( )| A. | 20° | B. | 30° | C. | 35° | D. | 50° |
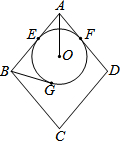 如图,菱形ABCD的边长为10,圆O分别与AB、AD相切于E、F两点,且与BG相切于G点.若AO=5,且圆O的半径为3,则BG的长度为何?( )
如图,菱形ABCD的边长为10,圆O分别与AB、AD相切于E、F两点,且与BG相切于G点.若AO=5,且圆O的半径为3,则BG的长度为何?( ) =__________(a<0)
=__________(a<0)