题目内容
9. 问题提出:如图,已知:线段AB,试在平面内找到符合条件的所有点C,使∠ACB=30°.(利用直尺和圆规作图,保留作图痕迹,不写作法).
问题提出:如图,已知:线段AB,试在平面内找到符合条件的所有点C,使∠ACB=30°.(利用直尺和圆规作图,保留作图痕迹,不写作法).尝试解决:为了解决这个问题,下面给出一种解题思路:先作出等边三角形AOB,然后以点O 为圆心,OA长为半径作⊙O,则优弧AB上的点即为所要求作的点(点A、B除外),根据对称性,在AB的另一侧符合条件的点C易得.请根据提示,完成作图.
自主探索:在平面直角坐标系中,已知点A(3,0)、B(-1,0),点C是y轴上的一个动点,当∠BCA=45°时,点C的坐标为(0,2+$\sqrt{7}$)或(0,-2-$\sqrt{7}$).
分析 (1)利用题中所给思路画出两段优弧即可;
(2)类似(1)中的画法作出满足条件的C点,如图2,然后利用勾股定理计算出CD的长,从而确定C点坐标,利用对称可得到C′点的坐标.
解答 解:(1)如图1,两段优弧(不含A、B两端点)为所作;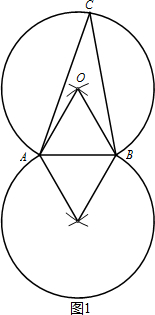
(2)如图2,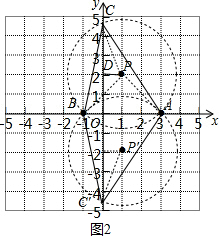
先作等腰直角△PAB,再以P点为圆心,PA为半径作⊙O交y轴于C点,
作PD⊥y轴于D,易得P(1,2),PA=2$\sqrt{2}$,
∴PC=2$\sqrt{2}$,
∴CD=$\sqrt{(2\sqrt{2})^{2}-{1}^{2}}$=$\sqrt{7}$,
∴OC=2+$\sqrt{7}$,
∴C(0,2+$\sqrt{7}$),
同理可得C′(0,-2-$\sqrt{7}$),
综上所述,满足条件的C点坐标为C(0,2+$\sqrt{7}$)或(0,-2-$\sqrt{7}$).
故答案为(0,2+$\sqrt{7}$)或(0,-2-$\sqrt{7}$).
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.解决本题的关键是圆周角定理的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下列各组中,是同类项的是( )
①23和32 ②-2p2t与tp2 ③-a2bcd与3b2acd ④$\frac{2}{3}{b}^{2}a与(-2)^{2}a{b}^{2}$.
①23和32 ②-2p2t与tp2 ③-a2bcd与3b2acd ④$\frac{2}{3}{b}^{2}a与(-2)^{2}a{b}^{2}$.
| A. | ② | B. | ②④ | C. | ①②④ | D. | ①②③④ |
14.不改变分式的值,下列各式中成立的是( )
| A. | $\frac{-a+5}{-a-5}=\frac{a+5}{a-5}$ | B. | $\frac{1}{-x+6}=\frac{-1}{x+6}$ | ||
| C. | $\frac{-x+y}{-x-y}=-\frac{x-y}{x+y}$ | D. | $\frac{-x}{y-3x}=\frac{x}{3x-y}$ |
18.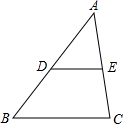 如图,在△ABC中,D、E分别是线段AB、AC的中点,则△ABC与△ADE的面积之比为( )
如图,在△ABC中,D、E分别是线段AB、AC的中点,则△ABC与△ADE的面积之比为( )
 如图,在△ABC中,D、E分别是线段AB、AC的中点,则△ABC与△ADE的面积之比为( )
如图,在△ABC中,D、E分别是线段AB、AC的中点,则△ABC与△ADE的面积之比为( )| A. | 1:2 | B. | 1:4 | C. | 4:1 | D. | 2:1 |
19.下列三个结论中正确的是( )
| A. | 2<$\sqrt{6}$<$\root{3}{7}$ | B. | 2<$\root{3}{7}$<$\sqrt{6}$ | C. | $\root{3}{7}$<2$<\sqrt{6}$ | D. | $\root{3}{7}$<$\sqrt{6}$<2 |
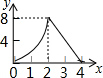
 如图,正方形ABCD的边长为4,动点M、N同时从A点出发,点M沿AB以每秒1个单位长度的速度向中点B运动,点N沿折现ADC以每秒2个单位长度的速度向终点C运动,设运动时间为t秒,则△CMN的面积为S关于t函数的图象大致是( )
如图,正方形ABCD的边长为4,动点M、N同时从A点出发,点M沿AB以每秒1个单位长度的速度向中点B运动,点N沿折现ADC以每秒2个单位长度的速度向终点C运动,设运动时间为t秒,则△CMN的面积为S关于t函数的图象大致是( )