题目内容
4.如图△ABC中,∠B=60°,∠C=78°,点D在AB边上,点E在AC边上,且DE∥BC,将△ADE沿DE折叠,点A对应点为F点.(1)若点A落在BC边上(如图1),求证:△BDF是等边三角形;
(2)若点A落在三角形外(如图2),且CF∥AB,求△CEF各内角的度数.

分析 (1)利用平行线的性质得出∠ADE=60°,再利用翻折变换的性质得出∠ADE=∠EDF=60°,进而得出∠BDF=60°即可得出答案;
(2)利用平行线的性质结合(1)中所求得出∠2,∠5+∠6的度数即可得出答案.
解答 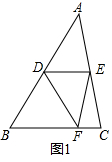 (1)证明:如图1,∵∠B=60°,DE∥BC,
(1)证明:如图1,∵∠B=60°,DE∥BC,
∴∠ADE=60°,
∵△ADE沿DE折叠,点A对应点为F点,
∴∠ADE=∠EDF=60°,
∴∠BDF=60°,
∴△BDF是等边三角形;
(2)解:如图2,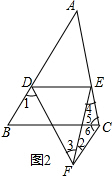 由(1)得:∠1=60°,
由(1)得:∠1=60°,
∵CF∥AB,
∴∠2+∠3=60°,∠B=∠6=60°,
∵∠B=60°,∠C=78°,
∴∠A=∠3=42°,
∴∠2=60°-42°=18°,
∴∠5+∠6=60°+78°=138°,
∴∠4=∠180°-18°-138°=24°.
点评 此题主要考查了翻折变换的性质以及平行线的性质和等边三角形的判定以及三角形内角和定理等知识,正确利用翻折变换的性质得出∠ADE=∠EDF是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.一袋面粉的质量标识为“25±0.25千克”,则下列一袋面粉质量中,合格的是( )
| A. | 25.30千克 | B. | 24.70千克 | C. | 25.51千克 | D. | 24.80千克 |
16.在平面直角坐标系xOy中,点P(-2,3)关于x轴的对称点坐标是( )
| A. | (-2,-3) | B. | (2,-3) | C. | (2,3) | D. | (-3,-2) |
13.下列各式计算正确的是( )
| A. | a0=1 | B. | (-3)-2=-$\frac{1}{9}$ | C. | $\sqrt{18}$-$\sqrt{32}$=-$\sqrt{2}$ | D. | $\sqrt{(-2)^{2}}$=-2 |
 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AB上的一个动点,DE⊥AC于点E.DF⊥BC于点F,点D从点A出发向点B移动(不含A、B两点),若AD长为x,矩形DECF的周长为y,则下列图象能大致反映y与x的函数关系的是( )
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AB上的一个动点,DE⊥AC于点E.DF⊥BC于点F,点D从点A出发向点B移动(不含A、B两点),若AD长为x,矩形DECF的周长为y,则下列图象能大致反映y与x的函数关系的是( )



 阅读下列材料:
阅读下列材料: 问题提出:如图,已知:线段AB,试在平面内找到符合条件的所有点C,使∠ACB=30°.(利用直尺和圆规作图,保留作图痕迹,不写作法).
问题提出:如图,已知:线段AB,试在平面内找到符合条件的所有点C,使∠ACB=30°.(利用直尺和圆规作图,保留作图痕迹,不写作法). 请在所给网格中按下列要求操作:
请在所给网格中按下列要求操作: