如图.在△ABC中.D.E分别是线段AB.AC的中点.则△ABC与△ADE的面积之比为( )A．1:2B．1:4C．4:1D．2:1 题目和参考答案——青夏教育精英家教网—

题目内容

18．

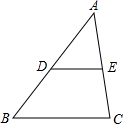如图，在△ABC中，D、E分别是线段AB、AC的中点，则△ABC与△ADE的面积之比为（　　）

A．

1：2

B．

1：4

C．

4：1

D．

2：1

分析根据三角形的中位线得出DE=$\frac{1}{2}$BC，DE∥BC，推出△ADE∽△ABC，根据相似三角形的性质得出即可．

解答解：∵D、E分别为AB、AC的中点，
∴BC=2DE，DE∥BC，
∴△ADE∽△ABC，
∴△ABC与△ADE的面积之比=（$\frac{BC}{DE}$）²=4：1．
故选C．

点评本题考查了三角形的性质和判定，三角形的中位线的应用，注意：相似三角形的面积比等于相似比的平方．

练习册系列答案

中考必备河南中考试题精选精析卷系列答案

9．

问题提出：如图，已知：线段AB，试在平面内找到符合条件的所有点C，使∠ACB=30°．（利用直尺和圆规作图，保留作图痕迹，不写作法）．
尝试解决：为了解决这个问题，下面给出一种解题思路：先作出等边三角形AOB，然后以点O 为圆心，OA长为半径作⊙O，则优弧AB上的点即为所要求作的点（点A、B除外），根据对称性，在AB的另一侧符合条件的点C易得．请根据提示，完成作图．
自主探索：在平面直角坐标系中，已知点A（3，0）、B（-1，0），点C是y轴上的一个动点，当∠BCA=45°时，点C的坐标为（0，2+$\sqrt{7}$）或（0，-2-$\sqrt{7}$）．

6．无锡地铁3号线预计全长约42500米，将42500用科学记数法表示为4.25×10⁴．

13．下列各式计算正确的是（　　）

A．

a⁰=1

B．

（-3）^-2=-$\frac{1}{9}$

C．

$\sqrt{18}$-$\sqrt{32}$=-$\sqrt{2}$

D．

$\sqrt{（-2）^{2}}$=-2

3．已知BD、CE分别是△ABC的AC边、AB边上的高，M是BC边的中点，分别联结MD、ME、DE．

（1）当∠BAC＜90°时，垂足D、E分别落在边AC、AB上，如图1，求证：DM=EM．
（2）若∠BAC=135°，试判断△DEM的形状，简写解答过程．
（3）当∠BAC＞90°时，设∠BAC的度数为x，∠DME的度数为y，求y与x之间的函数关系式．

10．如图是一个数值运算程序，当输入值为-1时，则输出的数值为（　　）

7．对于两个不相等的实数a、b，定义一种新的运算如下：a*b=$\frac{{\sqrt{a+b}}}{a-b}$（a+b＞0），如：3*2=$\frac{{\sqrt{3+2}}}{3-2}=\sqrt{5}$，那么15*（6*3）=$\frac{2}{7}$．

8．

如图，若点C是AB的黄金分割点，AC＞BC，AB=2，则AC的长为1.24（结果精确到0.01）．

试题分类