题目内容
19．
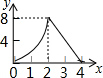如图，正方形ABCD的边长为4，动点M、N同时从A点出发，点M沿AB以每秒1个单位长度的速度向中点B运动，点N沿折现ADC以每秒2个单位长度的速度向终点C运动，设运动时间为t秒，则△CMN的面积为S关于t函数的图象大致是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 当0≤t≤2时，AM=t，AN=2t，利用S=S正方形ABCD-S△AMN-S△BCM-S△CDN可得到S=-t2+6t；当2＜t≤4时，CN=8-2t，利用三角形面积公式可得S=-4t+16，于是可判断当0≤t≤2时，S关于t函数的图象为开口向上的抛物线的一部分，当2＜t≤4时，S关于t函数的图象为一次函数图象的一部分，然后利用此特征对四个选项进行判断．
解答 解：当0≤t≤2时，AM=t，AN=2t，
所以S=S正方形ABCD-S△AMN-S△BCM-S△CDN=4×4-$\frac{1}{2}$•t•2t-$\frac{1}{2}$•4•（4-t）-$\frac{1}{2}$•4•（4-2t）=-t2+6t；
当2＜t≤4时，CN=8-2t，S=$\frac{1}{2}$•（8-2t）•4=-4t+16，
即当0≤t≤2时，S关于t函数的图象为开口向下的抛物线的一部分，当2＜t≤4时，S关于t函数的图象为一次函数图象的一部分．
故选D．
点评 本题考查了动点问题的函数图象：函数图象是典型的数形结合，图象应用信息广泛，通过看图获取信息，不仅可以解决生活中的实际问题，还可以提高分析问题、解决问题的能力．解决本题的关键是利用分类讨论的思想求出S与t的函数关系式．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，△ABD，△ACE都是等边三角形，点C在BD上，则∠ADE=60°．
10．
如图，在矩形ABCD中，两条对角线AC与BD相交于点O，AB=6，OA=4，则AD的长为（ ）
如图，在矩形ABCD中，两条对角线AC与BD相交于点O，AB=6，OA=4，则AD的长为（ ）| A． | 4 | B． | 8 | C． | 3$\sqrt{3}$ | D． | 2$\sqrt{7}$ |
7．在以下图形中，是中心对称图形的有（ ）
①圆 ②正方形 ③长方形 ④平行四边形 ⑤等边三角形．
①圆 ②正方形 ③长方形 ④平行四边形 ⑤等边三角形．
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
如图，在Rt△ABC中，∠C=90°，AC=4，BC=3，点D是AB上的一个动点，DE⊥AC于点E．DF⊥BC于点F，点D从点A出发向点B移动（不含A、B两点），若AD长为x，矩形DECF的周长为y，则下列图象能大致反映y与x的函数关系的是（ ）
11．
如图是一个正方体的展开图，标注了字母A的面是正方体的正面，如果正方体的左面和右面所标数字相等，则x的值是（ ）
如图是一个正方体的展开图，标注了字母A的面是正方体的正面，如果正方体的左面和右面所标数字相等，则x的值是（ ）| A． | 6 | B． | 1 | C． | $-\frac{1}{2}$ | D． | 0 |
问题提出：如图，已知：线段AB，试在平面内找到符合条件的所有点C，使∠ACB=30°．（利用直尺和圆规作图，保留作图痕迹，不写作法）．