题目内容
1. 如图,已知E、F、G、H分别是矩形四边AB、BC、CD、DA的中点,且四边形EFGH的周长为16cm,则矩形ABCD的对角线长等于8cm.
如图,已知E、F、G、H分别是矩形四边AB、BC、CD、DA的中点,且四边形EFGH的周长为16cm,则矩形ABCD的对角线长等于8cm.
分析 连接AC、BD,根据三角形的中位线求出HG、GF、EF、EH的长,即可得到四边形EFGH的周长与AC、BD的数量关系.
解答 解:如图,连接AC、BD,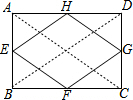
∵四边形ABCD是矩形,
∴AC=BD=8cm,
∵E、F、G、H分别是AB、BC、CD、DA的中点,
∴HG=EF=$\frac{1}{2}$AC,EH=FG=$\frac{1}{2}$BD,
∴四边形EFGH的周长等于HG+EF+EH+FG=4×$\frac{1}{2}$AC=16,
则AC=8cm
故答案为:8.
点评 本题考查了矩形的性质,三角形的中位线的应用,能求出四边形的各个边的长是解此题的关键,注意:矩形的对角线相等,三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
2.列方程组解应用题:
在“某地大地震”灾民安置工作中,某企业捐助了一批板材24 000m2,某灾民安置点用该企业捐助的这批板材全部搭建成A,B两种型号的板房,供2 300名灾民临时居住.已知建一间A型板房和一间B型板房所需板材及能安置的人数如下表所示:
问:(1)该灾民安置点需搭建A型板房和B型板房各多少间?
(2)因对灾民人数估计不足,实际安置中A型板房超员15%,B型板房超员20%,则该安置点灾民实际有多少人?
在“某地大地震”灾民安置工作中,某企业捐助了一批板材24 000m2,某灾民安置点用该企业捐助的这批板材全部搭建成A,B两种型号的板房,供2 300名灾民临时居住.已知建一间A型板房和一间B型板房所需板材及能安置的人数如下表所示:
| 板房型号 | 所需板材 | 安置人数 |
| A型板房 | 54m2 | 5 |
| B型板房 | 78m2 | 8 |
(2)因对灾民人数估计不足,实际安置中A型板房超员15%,B型板房超员20%,则该安置点灾民实际有多少人?
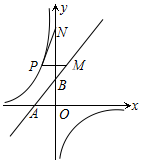 在平面直角坐标系中,已知点A(-$\sqrt{2}$,0)、B(0,$\sqrt{2}$)、N(0,3$\sqrt{2}$),P是反比例函数y=-$\frac{1}{x}$(x<0)的图象上一动点,PM∥x轴交直线AB于M,则PM+PN的最小值为$\frac{7\sqrt{2}}{3}$.
在平面直角坐标系中,已知点A(-$\sqrt{2}$,0)、B(0,$\sqrt{2}$)、N(0,3$\sqrt{2}$),P是反比例函数y=-$\frac{1}{x}$(x<0)的图象上一动点,PM∥x轴交直线AB于M,则PM+PN的最小值为$\frac{7\sqrt{2}}{3}$.
 如图,P为正方形ABCD 的边AD上的一动点,AE⊥BP,CF⊥BP,垂足分别为点E、F,已知AD=4.
如图,P为正方形ABCD 的边AD上的一动点,AE⊥BP,CF⊥BP,垂足分别为点E、F,已知AD=4.