题目内容
9.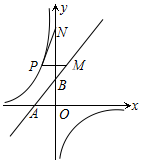 在平面直角坐标系中,已知点A(-$\sqrt{2}$,0)、B(0,$\sqrt{2}$)、N(0,3$\sqrt{2}$),P是反比例函数y=-$\frac{1}{x}$(x<0)的图象上一动点,PM∥x轴交直线AB于M,则PM+PN的最小值为$\frac{7\sqrt{2}}{3}$.
在平面直角坐标系中,已知点A(-$\sqrt{2}$,0)、B(0,$\sqrt{2}$)、N(0,3$\sqrt{2}$),P是反比例函数y=-$\frac{1}{x}$(x<0)的图象上一动点,PM∥x轴交直线AB于M,则PM+PN的最小值为$\frac{7\sqrt{2}}{3}$.
分析 先设出点P的坐标,进而表示出点M的坐标,再确定出点M关于点P的对称点M'的坐标,再判断出点M',P,N在同一条直线上时,PM+PN最小即可.
解答 解:∵A(-$\sqrt{2}$,0)、B(0,$\sqrt{2}$),
∴直线AB的解析式为y=x+$\sqrt{2}$,
设点P(m,-$\frac{1}{m}$),
∵PM∥x轴,
∴M(-$\sqrt{2}$-$\frac{1}{m}$,-$\frac{1}{m}$),
∴点M关于点P的对称点M'(2m+$\sqrt{2}$+$\frac{1}{m}$,-$\frac{1}{m}$),
∴PM+PN=PM'+PN,
∴点M',P,N在同一条直线上时,
即:-$\frac{1}{m}$=3$\sqrt{2}$,
∴m=-$\frac{\sqrt{2}}{6}$时,PM+PN最小=PM'+MN=M'N=|xM'|=|2m+$\sqrt{2}$+$\frac{1}{m}$|=$\frac{7\sqrt{2}}{3}$,
故答案为$\frac{7\sqrt{2}}{3}$.
点评 此题主要考查了待定系数法,对称的性质,极值的确定方法,解本题的关键是确定出点M',P,N在同一条直线上时,PM+PN最小.

练习册系列答案
相关题目
10.用科学记数法表示0.000034,结果是( )
| A. | 3.4×10-5 | B. | 3.4×10-4 | C. | 0.34×10-4 | D. | 34×10-6 |
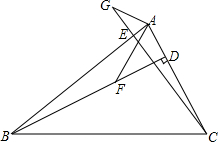 如图,已知在△ABC中,BD⊥AC于D,CE⊥AB于E,F是BD上一点,BF=AC,G是CE延长线上一点,CG=AB,连接AG,AF.
如图,已知在△ABC中,BD⊥AC于D,CE⊥AB于E,F是BD上一点,BF=AC,G是CE延长线上一点,CG=AB,连接AG,AF.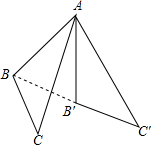 △ABC以点A为旋转中心,按逆时针方向旋转60°,得△AB′C′,则∠BAB′的度数是60°.
△ABC以点A为旋转中心,按逆时针方向旋转60°,得△AB′C′,则∠BAB′的度数是60°. 如图,已知E、F、G、H分别是矩形四边AB、BC、CD、DA的中点,且四边形EFGH的周长为16cm,则矩形ABCD的对角线长等于8cm.
如图,已知E、F、G、H分别是矩形四边AB、BC、CD、DA的中点,且四边形EFGH的周长为16cm,则矩形ABCD的对角线长等于8cm.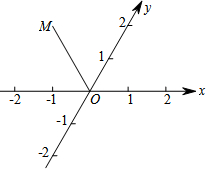 在平面上,过一定点O作两条斜交的轴x和y,它们的交角是ω(ω≠90°),以定点O为原点,在每条轴上取相同的单位长度,这样就在平面上建立了一个斜角坐标系,其中ω叫做坐标角.对于平面内任意一点P,过P作x轴和y轴的平行线,与两轴分别交于A和B,它们在两轴的坐标分别是x和y,于是点P的坐标就是(x,y).如图,ω=60°,且y轴平分∠MOx,OM=2,则点M的坐标是( )
在平面上,过一定点O作两条斜交的轴x和y,它们的交角是ω(ω≠90°),以定点O为原点,在每条轴上取相同的单位长度,这样就在平面上建立了一个斜角坐标系,其中ω叫做坐标角.对于平面内任意一点P,过P作x轴和y轴的平行线,与两轴分别交于A和B,它们在两轴的坐标分别是x和y,于是点P的坐标就是(x,y).如图,ω=60°,且y轴平分∠MOx,OM=2,则点M的坐标是( )