题目内容
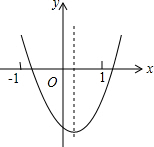 二次函数y=ax2+bx+c的图象如图所示,则abc,4ac-b2,2a+b,a-b+c这四个式子中,值为负数的有( )
二次函数y=ax2+bx+c的图象如图所示,则abc,4ac-b2,2a+b,a-b+c这四个式子中,值为负数的有( )| A、4个 | B、3个 | C、2个 | D、1 |
考点:二次函数图象与系数的关系
专题:数形结合
分析:由抛物线开口方向可得a>0,由抛物线的对称轴在y轴右侧得b<0,由抛物线与y轴的交点在x轴下方得c<0,所以abc>0;根据抛物线与x轴的交点个数得到△=b2-4ac>0,则4ac-b2<0;利用抛物线的对称轴的位置得0<-
<1,而a>0,利用不等式的性质变形得到2a+b>0;利用当x=-1时,函数值为正得到a-b+c>0.
| b |
| 2a |
解答:解:∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴为直线x=-
>0,
∴b<0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc>0;
∵抛物线与x轴有2个交点,
∴△=b2-4ac>0,
∴4ac-b2<0;
∵0<-
<1,而a>0,
∴-b<2a,即2a+b>0;
∵当x=-1时,y>0,
∴a-b+c>0,
即在abc,4ac-b2,2a+b,a-b+c这四个式子中,值为负数为4ac-b2.
故选D.
∴a>0,
∵抛物线的对称轴为直线x=-
| b |
| 2a |
∴b<0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc>0;
∵抛物线与x轴有2个交点,
∴△=b2-4ac>0,
∴4ac-b2<0;
∵0<-
| b |
| 2a |
∴-b<2a,即2a+b>0;
∵当x=-1时,y>0,
∴a-b+c>0,
即在abc,4ac-b2,2a+b,a-b+c这四个式子中,值为负数为4ac-b2.
故选D.
点评:本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点,抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
二次函数y=x2的图象向左平移2个单位,得到新的图象的二次函数表达式是( )
| A、y=x2+2 |
| B、y=(x+2)2 |
| C、y=(x-2)2 |
| D、y=x2-2 |
 二次函数y=ax2+bx+c的图象如图所示.当y>0时,自变量x的取值范围是( )
二次函数y=ax2+bx+c的图象如图所示.当y>0时,自变量x的取值范围是( )| A、-3<x<1 |
| B、x<-1 |
| C、x>3 |
| D、x<-3或x>1 |
已知抛物线y=x2-3x+1的图象上有一点(m,2),则代数式m2-3m+2014的值为( )
| A、2012 | B、2013 |
| C、2014 | D、2015 |