题目内容
解方程
(1)(2x+1)2=3(2x+1)
(2)先化简,再求值:
(x-1)÷(
-1),其中x为方程x2+3x+2=0的根.
(1)(2x+1)2=3(2x+1)
(2)先化简,再求值:
(x-1)÷(
| 2 |
| x+1 |
考点:分式的化简求值,解一元二次方程-因式分解法
专题:计算题
分析:(1)方程整理后,利用因式分解法求出解即可;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,求出方程的解得到x的值,代入原式计算即可得到结果.
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,求出方程的解得到x的值,代入原式计算即可得到结果.
解答:解:(1)方程移项得:(2x+1)2-3(2x+1)=0,
分解因式得:(2x+1)(2x+1-3)=0,
解得:x1=-
,x2=1;
(2)原式=(x-1)÷
=(x-1)•
=-x-1,
方程x2+3x+2=0,解得:x=-1或x=-2,
当x=-1时,原式没有意义;
当x=-2时,原式=1.
分解因式得:(2x+1)(2x+1-3)=0,
解得:x1=-
| 1 |
| 2 |
(2)原式=(x-1)÷
| 2-x-1 |
| x+1 |
| x+1 |
| -(x-1) |
方程x2+3x+2=0,解得:x=-1或x=-2,
当x=-1时,原式没有意义;
当x=-2时,原式=1.
点评:此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
 如图,AB∥CD,那么( )
如图,AB∥CD,那么( )| A、∠1=∠4 |
| B、∠1=∠3 |
| C、∠2=∠3 |
| D、∠1=∠5 |
下列函数中是二次函数的为( )
| A、y=3x-1 |
| B、y=3x2-1 |
| C、y=(x+1)2-x2 |
| D、y=x3+2x-3 |
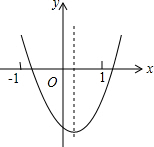 二次函数y=ax2+bx+c的图象如图所示,则abc,4ac-b2,2a+b,a-b+c这四个式子中,值为负数的有( )
二次函数y=ax2+bx+c的图象如图所示,则abc,4ac-b2,2a+b,a-b+c这四个式子中,值为负数的有( )| A、4个 | B、3个 | C、2个 | D、1 |
 如图,在函数y=-
如图,在函数y=-| 3 |
| x |
| A、S1>S2>S3 |
| B、S1<S2<S3 |
| C、S1<S3<S2 |
| D、S1=S2=S3 |