题目内容
1.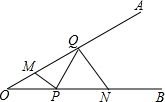 如图,∠AOB=30°,点M,N分别在边OA,OB上,OM=$\sqrt{7}$,ON=3$\sqrt{2}$,点P,Q分别在边OB,OA上运动,连接MP,PQ,QN,则MP+PQ+QN的最小值为5.
如图,∠AOB=30°,点M,N分别在边OA,OB上,OM=$\sqrt{7}$,ON=3$\sqrt{2}$,点P,Q分别在边OB,OA上运动,连接MP,PQ,QN,则MP+PQ+QN的最小值为5.
分析 作M关于OB的对称点M′,作N关于OA的对称点N′,连接M′N′,即为MP+PQ+QN的最小值.
解答 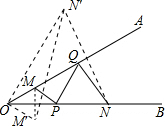 解:作M关于OB的对称点M′,作N关于OA的对称点N′,
解:作M关于OB的对称点M′,作N关于OA的对称点N′,
连接M′N′,即为MP+PQ+QN的最小值.
根据轴对称的定义可知:∠N′OQ=∠M′OB=30°,∠ONN′=60°,
∴△ONN′为等边三角形,△OMM′为等边三角形,
∴∠N′OM′=90°,
∴在Rt△M′ON′中,
M′N′=$\sqrt{(\sqrt{7})^{2}+(3\sqrt{2})^{2}}$=5.
故答案为5.
点评 本题考查了轴对称--最短路径问题,根据轴对称的定义,找到相等的线段,得到等边三角形是解题的关键.

练习册系列答案
相关题目
12.由线段a,b,c组成的三角形不是直角三角形的是( )
| A. | a=3,b=5,c=4 | B. | a=12,b=14,c=15 | C. | a=$\sqrt{41}$,b=4,c=5 | D. | a=9,b=41,c=40 |
16.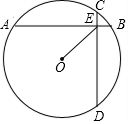 如图,在半径为6的⊙O内有两条互相垂直的弦AB和CD,AB=8,CD=6,垂足为E.则tan∠OEA的值是( )
如图,在半径为6的⊙O内有两条互相垂直的弦AB和CD,AB=8,CD=6,垂足为E.则tan∠OEA的值是( )
 如图,在半径为6的⊙O内有两条互相垂直的弦AB和CD,AB=8,CD=6,垂足为E.则tan∠OEA的值是( )
如图,在半径为6的⊙O内有两条互相垂直的弦AB和CD,AB=8,CD=6,垂足为E.则tan∠OEA的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{15}}{6}$ | D. | $\frac{2\sqrt{15}}{9}$ |
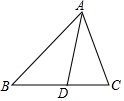 如图,在△ABC中,AD平分∠BAC交边BC于点D,BD=AD,AB=3,AC=2,那么AD的长是$\frac{3}{5}\sqrt{10}$.
如图,在△ABC中,AD平分∠BAC交边BC于点D,BD=AD,AB=3,AC=2,那么AD的长是$\frac{3}{5}\sqrt{10}$.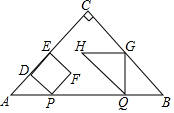 如图,△ABC是等腰直角三角形,∠ACB=90°,AB=4cm,动点P以1cm/s的速度分别从点A、B同时出发,点P沿A→B向终点B运动,点Q沿B→A向终点A运动,过点P作PD⊥AC于点D,以PD为边向右侧作正方形PDEF,过点Q作QG⊥AB,交折线BC-CA于点G与点C不重合,以QG为边作等腰直角△QGH,且点G为直角顶点,点C、H始终在QG的同侧,设正方形PDEF与△QGH重叠部分图形的面积为S(cm2),点P运动的时间为t(s)(0<t<4).
如图,△ABC是等腰直角三角形,∠ACB=90°,AB=4cm,动点P以1cm/s的速度分别从点A、B同时出发,点P沿A→B向终点B运动,点Q沿B→A向终点A运动,过点P作PD⊥AC于点D,以PD为边向右侧作正方形PDEF,过点Q作QG⊥AB,交折线BC-CA于点G与点C不重合,以QG为边作等腰直角△QGH,且点G为直角顶点,点C、H始终在QG的同侧,设正方形PDEF与△QGH重叠部分图形的面积为S(cm2),点P运动的时间为t(s)(0<t<4). 如图,在四边形ABCD中,动点P从点A开始沿A→B→C→D的路径匀速前进到D为止.在这个过程中,△APD的面积S随时间t的变化关系用图象表示正确的是( )
如图,在四边形ABCD中,动点P从点A开始沿A→B→C→D的路径匀速前进到D为止.在这个过程中,△APD的面积S随时间t的变化关系用图象表示正确的是( )


