题目内容
10．已知三角形的三条边的长度分别是：①10，24，26；②$\sqrt{3}$，$\sqrt{7}$，$\sqrt{10}$；③$\sqrt{3}$，$\sqrt{4}$，$\sqrt{5}$．其中能构成直角三角形的组数为（ ）| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
分析 先求得三边的平方，再验证两小边的平方和等于最长边的平方即可．
解答 解：①102+242=262，故是直角三角形；
②（$\sqrt{3}$）2+（$\sqrt{7}$）2=（$\sqrt{10}$）2，故是直角三角形；
③（$\sqrt{3}$）2+（$\sqrt{4}$）2≠（$\sqrt{5}$）2，故不是直角三角形．
故选：C．
点评 本题考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．
练习册系列答案
阅读快车系列答案
相关题目
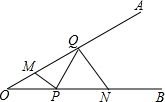如图，∠AOB=30°，点M，N分别在边OA，OB上，OM=$\sqrt{7}$，ON=3$\sqrt{2}$，点P，Q分别在边OB，OA上运动，连接MP，PQ，QN，则MP+PQ+QN的最小值为5．
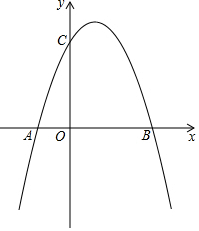如图，抛物线y=ax2+bx+c（a≠0）与x轴相交于A（-1，0），B（3，0），与y轴交于点C（0，3）．