题目内容
11.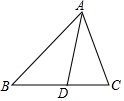 如图,在△ABC中,AD平分∠BAC交边BC于点D,BD=AD,AB=3,AC=2,那么AD的长是$\frac{3}{5}\sqrt{10}$.
如图,在△ABC中,AD平分∠BAC交边BC于点D,BD=AD,AB=3,AC=2,那么AD的长是$\frac{3}{5}\sqrt{10}$.
分析 根据题意得到△ACD∽△BCA,然后根据题目中的数据即可求得AD的长.
解答 解:∵在△ABC中,AD平分∠BAC交边BC于点D,BD=AD,
∴∠BAD=∠CAD,∠BAD=∠ABD,
∴∠ABC=∠CAD,
又∵∠ACD=∠BCA,
∴△ACD∽△BCA,
∴$\frac{AD}{BA}=\frac{AC}{BC}=\frac{CD}{AC}$,
∵BD=AD,AB=3,AC=2,
∴$\frac{AD}{3}=\frac{2}{BD+CD}=\frac{CD}{2}$,
解得,AD=$\frac{3\sqrt{10}}{5}$,CD=$\frac{2\sqrt{10}}{5}$,
故答案为:$\frac{3\sqrt{10}}{5}$.
点评 本题考查相似三角形的判定与性质,解答本题的关键是明确题意,找出三角形相似的条件.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
16.下列调查中,适宜采用抽样调查方式的是( )
| A. | 调查札幌亚冬会女子越野滑雪1.4公里决赛参赛运动员兴奋剂的使用情况 | |
| B. | 调查中国民众对美国在韩部署萨德系统持反对态度的比例 | |
| C. | 调查中国国产航母各零部件的质量 | |
| D. | 调查某班学生对感动中国2016年度人物我校高2004级校友秦珇飞的知晓率 |
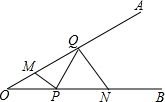 如图,∠AOB=30°,点M,N分别在边OA,OB上,OM=$\sqrt{7}$,ON=3$\sqrt{2}$,点P,Q分别在边OB,OA上运动,连接MP,PQ,QN,则MP+PQ+QN的最小值为5.
如图,∠AOB=30°,点M,N分别在边OA,OB上,OM=$\sqrt{7}$,ON=3$\sqrt{2}$,点P,Q分别在边OB,OA上运动,连接MP,PQ,QN,则MP+PQ+QN的最小值为5.