题目内容
6. 如图,在四边形ABCD中,动点P从点A开始沿A→B→C→D的路径匀速前进到D为止.在这个过程中,△APD的面积S随时间t的变化关系用图象表示正确的是( )
如图,在四边形ABCD中,动点P从点A开始沿A→B→C→D的路径匀速前进到D为止.在这个过程中,△APD的面积S随时间t的变化关系用图象表示正确的是( )| A. |  | B. |  | C. |  | D. |  |
分析 根据点P的运动过程可知:△APD的底边为AD,而且AD始终不变,点P到直线AD的距离为△APD的高,根据高的变化即可判断S与t的函数图象.
解答 解:设点P到直线AD的距离为h,
∴△APD的面积为:S=$\frac{1}{2}$AD•h,
当P在线段AB运动时,
此时h不断增大,S也不端增大
当P在线段BC上运动时,
此时h不变,S也不变,
当P在线段CD上运动时,
此时h不断减小,S不断减少,
又因为匀速行驶且CD>AB,所以在线段CD上运动的时间大于在线段AB上运动的时间
故选(C)
点评 本题考查函数图象,解题的关键是根据点P到直线AD的距离来判断s与t的关系,本题属于基础题型.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
16.下列调查中,适宜采用抽样调查方式的是( )
| A. | 调查札幌亚冬会女子越野滑雪1.4公里决赛参赛运动员兴奋剂的使用情况 | |
| B. | 调查中国民众对美国在韩部署萨德系统持反对态度的比例 | |
| C. | 调查中国国产航母各零部件的质量 | |
| D. | 调查某班学生对感动中国2016年度人物我校高2004级校友秦珇飞的知晓率 |
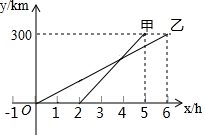 甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,乙出发2h后甲再出发,且甲、乙两人离A地的距离y甲、y乙与时间x之间的函数图象如图所示.
甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,乙出发2h后甲再出发,且甲、乙两人离A地的距离y甲、y乙与时间x之间的函数图象如图所示.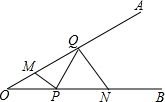 如图,∠AOB=30°,点M,N分别在边OA,OB上,OM=$\sqrt{7}$,ON=3$\sqrt{2}$,点P,Q分别在边OB,OA上运动,连接MP,PQ,QN,则MP+PQ+QN的最小值为5.
如图,∠AOB=30°,点M,N分别在边OA,OB上,OM=$\sqrt{7}$,ON=3$\sqrt{2}$,点P,Q分别在边OB,OA上运动,连接MP,PQ,QN,则MP+PQ+QN的最小值为5. 如图,在菱形ABCD中,EF∥BC,$\frac{AE}{BE}$=$\frac{1}{3}$,EF=3,则CD的长为12.
如图,在菱形ABCD中,EF∥BC,$\frac{AE}{BE}$=$\frac{1}{3}$,EF=3,则CD的长为12.