题目内容
14.若方程组$\left\{\begin{array}{l}{4x-y=5}\\{ax+by=-1}\end{array}\right.$ 与$\left\{\begin{array}{l}{3x+y=9}\\{3ax-4by=18}\end{array}\right.$有公共解,求a,b的值.分析 根据方程组$\left\{\begin{array}{l}{4x-y=5}\\{ax+by=-1}\end{array}\right.$ 与$\left\{\begin{array}{l}{3x+y=9}\\{3ax-4by=18}\end{array}\right.$有公共解,可知两个方程组中任意两个方程组成的方程组的解就是两个方程组的公共解,从而可以得到方程组$\left\{\begin{array}{l}{4x-y=5}\\{ax+by=-1}\end{array}\right.$,解得的方程组的解就是$\left\{\begin{array}{l}{3x+y=9}\\{3ax-4by=18}\end{array}\right.$的解,从而可以得到a、b的值.
解答 解:∵方程组$\left\{\begin{array}{l}{4x-y=5}\\{ax+by=-1}\end{array}\right.$ 与$\left\{\begin{array}{l}{3x+y=9}\\{3ax-4by=18}\end{array}\right.$有公共解,
∴$\left\{\begin{array}{l}{4x-y=5}\\{3x+y=9}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$,
将x=2,y=3代入$\left\{\begin{array}{l}{ax+by=-1}\\{3ax-4by=18}\end{array}\right.$,得
$\left\{\begin{array}{l}{2a+3b=-1}\\{6a-12b=18}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{b=-1}\end{array}\right.$,
即a、b的值分别是1,-1.
点评 本题考查二元一次方程组的解、解二元一次方程组,解题的关键是明确题意,知道二个二元一次方程组的公共解,适合任何一个二元一次方程,从而可以建立新的方程组进行解答.

| A. | x+y≠0 | B. | x=y | C. | x+y=0 | D. | x=$\frac{1}{y}$ |
| A. | 一组对边相等且平行的四边形是平行四边形 | |
| B. | 有两边相等的四边形是平行四边形 | |
| C. | 四个全等的三角形一定可组成一个平行四边形 | |
| D. | 一组对边平行,另一组对边相等的四边形是平行四边形 |
 如图,已知:a∥b,三角板的直角顶点在直线b上,∠1=40°,则∠2=50°.
如图,已知:a∥b,三角板的直角顶点在直线b上,∠1=40°,则∠2=50°.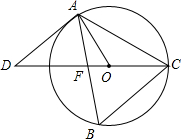 如图,△ABC内接于⊙O,∠B=66°,CE是⊙O的直径,点D是CE延长线上的一点.且∠D=42°.
如图,△ABC内接于⊙O,∠B=66°,CE是⊙O的直径,点D是CE延长线上的一点.且∠D=42°.