题目内容
2.小明、小强、小华、小丽、小红五位同学在操场玩击掌传球游戏.游戏规则如下:小红为击掌者.持球者将球传给其他三位中的一位算一次传球.接球者必须将球迅速传给其他三位中的一位.如果接球者在随机掌声停止时(击掌者背对传球者)未将球传出.那么要给大家即兴表演一个节目.(1)小明持球先开始传球.若第一次传球后掌声停止.求第一次传球后.小丽即兴表演节目的概率;
(2)小明持球先开始传球,若第三次传球后掌声停止.请你用画树状图的方法求小明即兴表演节目的概率.
分析 (1)根据概率公式求解可得;
(2)画树状图列出所有等可能结果,根据概率公式求解可得.
解答 解:(1)第一次传球后掌声停止,表演节目的有小强、小华、小丽三种情况,
∴小丽即兴表演节目的概率为$\frac{1}{3}$;
(2)设将小明、小强、小华、小丽分别记为A、B、C、D,
画树状图如下: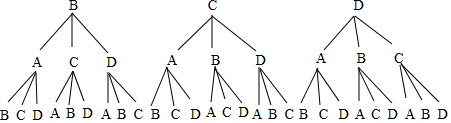
由树状图可知共有27种等可能结果,其中第三次传球后掌声停止时球落在小明手上的有6种结果,
∴小明即兴表演节目的概率为$\frac{6}{27}$=$\frac{2}{9}$.
点评 本题考查的是用列表法或画树状图法求概率.注意列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
10.自2014年12月28日北京公交地铁调价以来,人们的出行成本发生了较大的变化.小林根据新闻,将地铁和公交车的票价绘制成了如下两个表格.(说明:表格中“6~12公里”指的是大于6公里,小于等于12公里,其他类似)
根据以上信息回答下列问题:
小林办了一张市政交通一卡通学生卡,目前乘坐地铁没有折扣.
(1)如果小林全程乘坐地铁的里程为14公里,用他的学生卡需要刷卡交费5元;
(2)如果小林全程乘坐公交车的里程为16公里,用他的学生卡需要刷卡交费1元;
(3)小林用他的学生卡乘坐一段地铁后换乘公交车,两者累计里程为12公里.已知他乘坐地铁平均每公里花费0.4元,乘坐公交车平均每公里花费0.25元,此次行程共花费4.5元.请问小林乘坐地铁和公交车的里程分别是多少公里?

| 
| ||||||||||||||||||||||||||||||
小林办了一张市政交通一卡通学生卡,目前乘坐地铁没有折扣.
(1)如果小林全程乘坐地铁的里程为14公里,用他的学生卡需要刷卡交费5元;
(2)如果小林全程乘坐公交车的里程为16公里,用他的学生卡需要刷卡交费1元;
(3)小林用他的学生卡乘坐一段地铁后换乘公交车,两者累计里程为12公里.已知他乘坐地铁平均每公里花费0.4元,乘坐公交车平均每公里花费0.25元,此次行程共花费4.5元.请问小林乘坐地铁和公交车的里程分别是多少公里?
11.甲、乙、丙3人聚会,每人带了一件礼物,将这3件礼物分别放在3个完全相同的盒子里,每人随机抽取一个礼盒(装有礼物的盒子)
(1)下列事件是必然事件的是C
(2)甲、乙、丙3人抽到的都不是自己带来的礼物(记为事件A),请列出事件A的所有可能的结果,并求事件A的概率.
(1)下列事件是必然事件的是C
| A 乙没有抽到自己带来的礼物 | B 乙恰好抽到自己带来的礼物 |
| C 乙抽到一件礼物 | D 只有乙抽到自己带来的礼物 |
12. 如图,正方形ABCD中,AB=4,点E是边BC的中点,点G,H分别是边CD,AB上的动点,连接GH交AE于F,且使GH⊥AE,连接AG,EH,则EH+AG的最小值是( )
如图,正方形ABCD中,AB=4,点E是边BC的中点,点G,H分别是边CD,AB上的动点,连接GH交AE于F,且使GH⊥AE,连接AG,EH,则EH+AG的最小值是( )
 如图,正方形ABCD中,AB=4,点E是边BC的中点,点G,H分别是边CD,AB上的动点,连接GH交AE于F,且使GH⊥AE,连接AG,EH,则EH+AG的最小值是( )
如图,正方形ABCD中,AB=4,点E是边BC的中点,点G,H分别是边CD,AB上的动点,连接GH交AE于F,且使GH⊥AE,连接AG,EH,则EH+AG的最小值是( )| A. | 8 | B. | 4$\sqrt{5}$ | C. | 2$\sqrt{10}$ | D. | 8$\sqrt{2}$ |
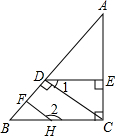 如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1与∠2互补,判断HF与AB是否垂直,并说明理由(填空)
如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1与∠2互补,判断HF与AB是否垂直,并说明理由(填空)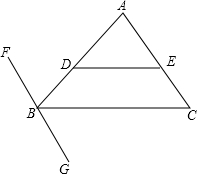 如图,点D、E分别在△ABC的边AB、AC上,且DE∥BC,过点B作直线FG,使∠CBG=∠AED,请判断FG与AC是否平行?并说明理由.
如图,点D、E分别在△ABC的边AB、AC上,且DE∥BC,过点B作直线FG,使∠CBG=∠AED,请判断FG与AC是否平行?并说明理由.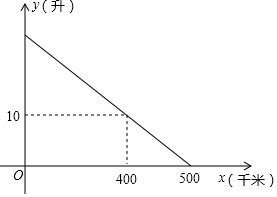 已知某汽车装满油后邮箱中的剩余油量y(升)与汽车的行驶路程x(千米)之间具有一次函数关系(如图所示),为了行驶安全考虑,邮箱中剩余油量不能低于5升,那么这辆汽车装满油后至多行驶450千米,就应该停车加油.
已知某汽车装满油后邮箱中的剩余油量y(升)与汽车的行驶路程x(千米)之间具有一次函数关系(如图所示),为了行驶安全考虑,邮箱中剩余油量不能低于5升,那么这辆汽车装满油后至多行驶450千米,就应该停车加油.