题目内容
14.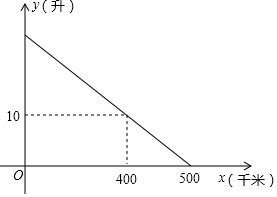 已知某汽车装满油后邮箱中的剩余油量y(升)与汽车的行驶路程x(千米)之间具有一次函数关系(如图所示),为了行驶安全考虑,邮箱中剩余油量不能低于5升,那么这辆汽车装满油后至多行驶450千米,就应该停车加油.
已知某汽车装满油后邮箱中的剩余油量y(升)与汽车的行驶路程x(千米)之间具有一次函数关系(如图所示),为了行驶安全考虑,邮箱中剩余油量不能低于5升,那么这辆汽车装满油后至多行驶450千米,就应该停车加油.
分析 根据函数图象中点的坐标利用待定系数法求出一次函数解析式,再根据一次函数图象上点的坐标特征即可求出剩余油量为5升时行驶的路程,此题得解.
解答 解:设该一次函数解析式为y=kx+b,
将(400,10)、(500,0)代入y=kx+b中,
$\left\{\begin{array}{l}{400k+b=10}\\{500k+b=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-0.1}\\{b=50}\end{array}\right.$,
∴该一次函数解析式为y=-0.1x+50.
当y=-0.1x+50=5时,x=450.
故答案为:450
点评 本题考查一次函数的应用、待定系数法求一次函数解析式以及一次函数图象上点的坐标特征,根据点的坐标利用待定系数法求出一次函数解析式是解题的关键.

练习册系列答案
相关题目
6.某班30名同学在“献爱心”活动中都捐赠了图书,各人捐赠的本数如下5,2,4,5,3,2,4,3,5,4,3,4,2,3,3,4,4,5,3,4,3,5,3,5,3,4,3,4,3,3.
(1)填写全班同学捐书册数统计表中未完成的部分.
(2)画出扇形统计图,描述分别捐赠2册、3册、4册和5册图书的人数占全班同学的百分比.
(1)填写全班同学捐书册数统计表中未完成的部分.
(2)画出扇形统计图,描述分别捐赠2册、3册、4册和5册图书的人数占全班同学的百分比.
| 捐书册数 | 划记 | 人数 | 百分比 |
| 2 |  | 3 | 10% |
| 3 |  | 12 | 40% |
| 4 |  | 9 | 30% |
| 5 |  | 6 | 20% |
3.下列选项中的图形,是轴对称图形但不是中心对称图形的是( )
| A. | 平行四边形 | B. | 正六边形 | C. | 直角三角形 | D. | 正三角形 |