题目内容
11.甲、乙、丙3人聚会,每人带了一件礼物,将这3件礼物分别放在3个完全相同的盒子里,每人随机抽取一个礼盒(装有礼物的盒子)(1)下列事件是必然事件的是C
| A 乙没有抽到自己带来的礼物 | B 乙恰好抽到自己带来的礼物 |
| C 乙抽到一件礼物 | D 只有乙抽到自己带来的礼物 |
分析 (1)根据事件发生的可能性大小判断相应事件的类型即可.
(2)画出树状图,然后根据概率公式列式计算即可得解.
解答 解:(1)A 乙没有抽到自己带来的礼物是随机事件;
B 乙恰好抽到自己带来的礼物是随机事件;
C 乙抽到一件礼物是必然事件;
D 只有乙抽到自己带来的礼物随机事件;
故选:C;
(2)设甲、乙、丙带的礼物分别记为A、B、C,
根据题意画出树状图如下:
一共有6种情况,其中甲、乙、丙3人抽到的都不是自己带来的礼物的情况共有(B、C、A)和(C、A、B)2种,
∴P(事件A)=$\frac{2}{6}$=$\frac{1}{3}$.
点评 此题考查了列表法与树状图法,解决问题的关键是掌握:概率=所求情况数与总情况数之比.解决本题需要正确理解必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件;不可能事件是指在一定条件下,一定不发生的事件;随机事件是指在一定条件下,可能发生也可能不发生的事件.

练习册系列答案
相关题目
6.某班30名同学在“献爱心”活动中都捐赠了图书,各人捐赠的本数如下5,2,4,5,3,2,4,3,5,4,3,4,2,3,3,4,4,5,3,4,3,5,3,5,3,4,3,4,3,3.
(1)填写全班同学捐书册数统计表中未完成的部分.
(2)画出扇形统计图,描述分别捐赠2册、3册、4册和5册图书的人数占全班同学的百分比.
(1)填写全班同学捐书册数统计表中未完成的部分.
(2)画出扇形统计图,描述分别捐赠2册、3册、4册和5册图书的人数占全班同学的百分比.
| 捐书册数 | 划记 | 人数 | 百分比 |
| 2 |  | 3 | 10% |
| 3 |  | 12 | 40% |
| 4 |  | 9 | 30% |
| 5 |  | 6 | 20% |
3.下列选项中的图形,是轴对称图形但不是中心对称图形的是( )
| A. | 平行四边形 | B. | 正六边形 | C. | 直角三角形 | D. | 正三角形 |
1.△ABC中AB=AC,AB的垂直平分线交AB于点D,交直线AC于点E,∠AEB=70°,那么∠BAC等于( )
| A. | 55° 或125° | B. | 65° | C. | 55° | D. | 125° |
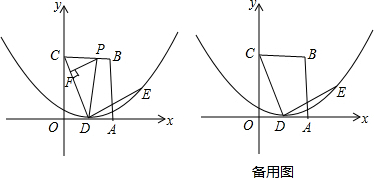
 如图,△ABC中,∠ACB=135°,AC=4,在同一平面内,将△ABC绕点C顺时针方向旋转到△A′B′C,使得AA′∥CB,则AA′的长度为4$\sqrt{2}$.
如图,△ABC中,∠ACB=135°,AC=4,在同一平面内,将△ABC绕点C顺时针方向旋转到△A′B′C,使得AA′∥CB,则AA′的长度为4$\sqrt{2}$.