题目内容
18.直线y1=k1x+4与双曲线y2=$\frac{{k}_{2}}{x}$交于点(3,1),(m,3),则当y1>y2时,自变量x的范围是( )| A. | 1<x<3 | B. | 0<x<1 | C. | x<0,1<x<3 | D. | 0<x<1,x>3 |
分析 根据点的坐标求出双曲线的解析式,得出另一个交点的坐标,利用函数图象即可确定出当y1>y2时的变量x的取值范围.
解答 解:如图所示 :
:
把点(3,1)代入双曲线y2=$\frac{{k}_{2}}{x}$得:k2=3,
∴双曲线解析式为y=$\frac{3}{x}$,
把(m,3)代入双曲线解析式为y=$\frac{3}{x}$得:m=1,
∴直线y1=k1x+4与双曲线y2=$\frac{{k}_{2}}{x}$交于点(3,1),(1,3),
根据图象得:当y1>y2时的变量x的取值范围为x<0,1<x<3.
故选C.
点评 此题考查了反比例函数与一次函数的交点问题,利用了数形结合的思想,熟练掌握数形结合思想是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8. 如图是一个几何体的三视图,则这个几何体的侧面积是( )
如图是一个几何体的三视图,则这个几何体的侧面积是( )
 如图是一个几何体的三视图,则这个几何体的侧面积是( )
如图是一个几何体的三视图,则这个几何体的侧面积是( )| A. | 9π | B. | 18π | C. | 27π | D. | 36π |
20.若一个角与它的余角相等,则这个角的度数为( )
| A. | 30° | B. | 35° | C. | 45° | D. | 60° |
 如图,在半圆BAC中,点O为圆心,OD⊥AB于D,OE⊥AC于E,连接DE,若DE=AB=2,则图中阴影部分的面积为2π-2$\sqrt{3}$(结果保留π)
如图,在半圆BAC中,点O为圆心,OD⊥AB于D,OE⊥AC于E,连接DE,若DE=AB=2,则图中阴影部分的面积为2π-2$\sqrt{3}$(结果保留π)



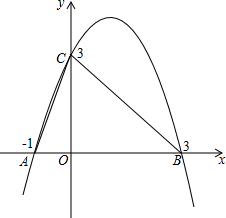 已知抛物线y=ax2+bx+c经过A(-1,0),B(3,0),C(0,3).
已知抛物线y=ax2+bx+c经过A(-1,0),B(3,0),C(0,3).