题目内容
20．
如图，在平行四边形ABCD中，E是CD延长线上一点，BE与AD交于F，若CD=2DE，则$\frac{{S}_{△DEF}}{{S}_{△ABF}}$等于（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{8}$ |
分析 由平行四边形的性质得出AB∥CD，AB=CD，证出△DEF∽△ABF，由相似三角形的面积比等于相似比的平方，即可得出结论．
解答 解：∵CD=2DE，
∴DE：CD=1：2，
∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD，
∴DE：AB=1：2，△DEF∽△ABF，
∴$\frac{{S}_{△DEF}}{{S}_{△ABF}}$=（$\frac{1}{2}$）2=$\frac{1}{4}$；
故选：C．
点评 本题考查了平行四边形的性质、相似三角形的判定与性质；熟练掌握平行四边形的性质，证明三角形相似得出面积比等于相似比的平方是解决问题的关键．
练习册系列答案
口算能手系列答案
相关题目
10．
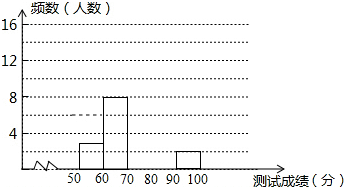为了增强学生法律意识，某校举办了首届“法律进校园，法在我心中”知识大赛，经选拔后有25名学生参加决赛，这25名学生同时解答50个选择题，若每正确一个选择题得2分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：
（1）求表中m的值；
（2）请把频数分布直方图补充完整；
（3）第4组的同学将抽出2名对第一组2名同学进行“一帮一”辅导，则第4组的小王与小李能同时抽到的概率是多少？
为了增强学生法律意识，某校举办了首届“法律进校园，法在我心中”知识大赛，经选拔后有25名学生参加决赛，这25名学生同时解答50个选择题，若每正确一个选择题得2分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：| 组别 | 成绩x分 | 频数（人数） |
| 第1组 | 50≤x＜60 | 3 |
| 第2组 | 60≤x＜70 | 7 |
| 第3组 | 70≤x＜80 | 10 |
| 第4组 | 80≤x＜90 | m |
| 第5组 | 90≤x＜100 | 2 |
（2）请把频数分布直方图补充完整；
（3）第4组的同学将抽出2名对第一组2名同学进行“一帮一”辅导，则第4组的小王与小李能同时抽到的概率是多少？
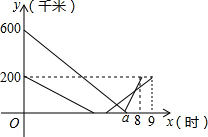甲、乙两车在连通A、B、C三地的公路上行驶，B地在A地、C地之间，甲车从A地出发匀速向C地行驶，同时乙车从C地出发匀速向B地行驶，到达B地并在B地停留1h后，按原路原速返回到C地．在两车行驶的过程中，甲、乙两车距B地的路程y（km）与行驶时间x（h）之间的函数图象如图所示．下列说法：