题目内容
13.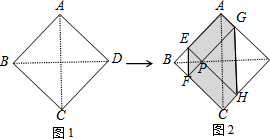 如图1,正方形纸片ABCD边长为2,折叠∠B和∠D,使两个直角的顶点重合于对角线BD上的一点P,EF、GH分别是折痕(图2).设AE=x(0<x<2),给出下列判断:
如图1,正方形纸片ABCD边长为2,折叠∠B和∠D,使两个直角的顶点重合于对角线BD上的一点P,EF、GH分别是折痕(图2).设AE=x(0<x<2),给出下列判断:①x=$\frac{1}{2}$时,EF+GH>AC;
②六边形AEFCHG面积的最大值是3;
③六边形AEFCHG周长的值为定值.
其中正确的是( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
分析 (1)由△BEF∽△BAC,得出EF=$\frac{3}{4}$AC,同理得出GH=$\frac{1}{4}$AC,从而得出结论;
(2)由六边形AEFCHG面积=正方形ABCD的面积-△EBF的面积-△GDH的面积.得出函数关系式,进而求出最大值;
(3)根据六边形AEFCHG周长=AE+EF+FC+CH+HG+AG=(AE+CH)+(FC+AG)+(EF+GH)求解即可.
解答 解:正方形纸片ABCD,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P,
∴△BEF∽△BAC,
∵x=$\frac{1}{2}$,
∴BE=2-$\frac{1}{2}$=$\frac{3}{2}$,
∴$\frac{EF}{AC}$=$\frac{BE}{BA}$=$\frac{\frac{3}{2}}{2}$=$\frac{3}{4}$,
∴EF=$\frac{3}{4}$AC,
同理,GH=$\frac{1}{4}$AC,
∴EF+GH=AC,①不正确;
六边形AEFCHG面积=正方形ABCD的面积-△EBF的面积-△GDH的面积.
∵AE=x,
∴六边形AEFCHG面积=22-$\frac{1}{2}$BE•BF-$\frac{1}{2}$GD•HD=4-$\frac{1}{2}$×(2-x)•(2-x)-$\frac{1}{2}$x•x=-x2+2x+2=-(x-1)2+3,
∴六边形AEFCHG面积的最大值是3,故②结论正确;
∵EF+GH=AC,
六边形AEFCHG周长=AE+EF+FC+CH+HG+AG=(AE+CH)+(FC+AG)+(EF+GH)=2+2+2$\sqrt{2}$=4+2$\sqrt{2}$,
故六边形AEFCHG周长的值不变,
故③结论正确.
故选:C.
点评 此题考查了翻折变换(折叠问题),菱形的性质,本题关键是得到EF+GH=AC,综合性较强,有一定的难度.

| A. | 144° | B. | 140° | C. | 135° | D. | 120° |
| A. | m>-4 | B. | m>-3 | C. | m<-4 | D. | m<-3 |
| A. | 平行四边形 | B. | 正方形 | C. | 矩形 | D. | 梯形 |
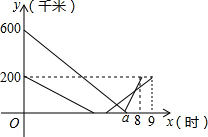 甲、乙两车在连通A、B、C三地的公路上行驶,B地在A地、C地之间,甲车从A地出发匀速向C地行驶,同时乙车从C地出发匀速向B地行驶,到达B地并在B地停留1h后,按原路原速返回到C地.在两车行驶的过程中,甲、乙两车距B地的路程y(km)与行驶时间x(h)之间的函数图象如图所示.下列说法:
甲、乙两车在连通A、B、C三地的公路上行驶,B地在A地、C地之间,甲车从A地出发匀速向C地行驶,同时乙车从C地出发匀速向B地行驶,到达B地并在B地停留1h后,按原路原速返回到C地.在两车行驶的过程中,甲、乙两车距B地的路程y(km)与行驶时间x(h)之间的函数图象如图所示.下列说法: