题目内容
2.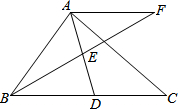 在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F
在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F(1)求证:△AEF≌△DEB;
(2)证明:四边形ADCF是菱形;
(3)若AB=4,AC=5,求菱形ADCF的面积.
分析 (1)根据AAS证明即可判定.
(2)先证明四边形ADCF是平行四边形,再证明DA=DC即可.
(3)利用S菱形ADCF=2S△ADC=S△ABC即可求解.
解答 (1)证明:∵AF∥BD,
∴∠AFE=∠DBE,
∵E是AD中点,
∴AE=ED,
在△BDE和△FAE中,
$\left\{\begin{array}{l}{∠AFE=∠DBE}\\{∠AEF=∠BED}\\{AE=ED}\end{array}\right.$,
∴△AFE≌△DBE.
(2)证明:连接CF. ∵△AFE≌△DBE,
∵△AFE≌△DBE,
∴AF=BD
∵∠BAC=90°,BD=CD,
∴AD=DC=DB,
∴AF∥CD,AF=DC,
∴四边形ADCF是平行四边形,
∵DA=CD,
∴四边形ADCF是菱形.
(3)∵S△ABC=$\frac{1}{2}$×AB×AC=10,
∵四边形ADCF是菱形,BD=DC,S△ABC=2S△ADC,
∴S菱形ADCF=2S△ADC=10.
点评 本题考查全等三角形的判定和性质、菱形的判定和性质,直角三角形斜边中线定理,解决问题的关键是记住菱形、全等三角形的判定方法,属于中考常考题型.

练习册系列答案
相关题目
14.半径为2的⊙O中,弦AB=2$\sqrt{3}$,弦AB所对的圆周角的度数为( )
| A. | 60° | B. | 60°或120° | C. | 45°或135° | D. | 30°或150° |
11.在下列各式中正确的是( )
| A. | $\sqrt{{{(-2)}^2}}$=-2 | B. | $±\sqrt{9}$=3 | C. | $\root{3}{-27}$=3 | D. | $\sqrt{2^2}$=2 |
12.下列计算正确的是( )
| A. | x3•x-4=x-12 | B. | (x3)3=x6 | C. | 2x2+x=x | D. | (3x)-2=$\frac{1}{9{x}^{2}}$ |
