题目内容
15.如图.在平面直角坐标系中,边长为1的正方形ABCD位于(1)的位置,顶点C与原点重合,把正方形绕点C顺时针旋转90°,使OB与x轴重合,得到正方形(2);把正方形(2)绕右下方的顶点顺时针旋转90°,得到正方形(3),按同样的变换方式,正方形依次经过(2),(3),(4),(5)…位置,点A依次经过A1,A2,A3,A4,A5,…
(1)填写下列各点的坐标:
A5(5,1),A6(6,0),A7(6,0);
(2)写出A2014的坐标(2014,0);
(3)求线段OA27的长.
分析 (1)观察图象即可得到答案.
(2)根据x轴上的点的下标的规律是4n+2或4n+3,不难求出点A2014的坐标.
(3)根据规律找到A27的位置,再确定OA27的长度.
解答 解:(1)由图象可知A5(5,1),A6(6,0),A7(6,0),
故答案为A5(5,1),A6(6,0),A7(6,0).
(2)∵A2(2,0),A3(2,0);A6(6,0),A7(6,0);A10(10,0),A11(10,0);…A4n+2(4n+2,0)A4n+3(4n+2,0),
又∵2014=503×4+2,
∴A2014(2014,0).
(3)∵27=6×4+3,
∴A27与A26坐标相同,
∴A27(26,0),
∴OA27=26.
点评 本题考查点的坐标,寻找点的坐标规律是解决问题的关键,学会从特殊到一般的发现规律数学思想,属于中考常考题型.

练习册系列答案
相关题目
10.M是线段AB的中点,P是MB上一点,PM等于( )
| A. | $\frac{1}{2}$(AM+PB) | B. | $\frac{1}{2}$(PA-PB) | C. | $\frac{1}{2}$AB-PB | D. | 以上都不对 |
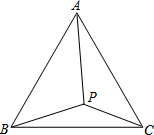 P为等边△ABC内一点,且∠APC=110°,∠BPC=132°,试求以AP、BP、CP为边的三角形的度数?
P为等边△ABC内一点,且∠APC=110°,∠BPC=132°,试求以AP、BP、CP为边的三角形的度数?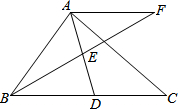 在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F
在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F