Question

4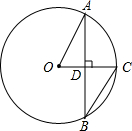．如图，⊙O的弦AB垂直半径OC于点D，∠CBA=30°，OC=2cm，则弦AB的长为（　　）

• A． 9cm
• B． 2$\sqrt{3}$cm
• C． $\frac{9}{2}$ cm
• D． $\frac{3\sqrt{3}}{2}$ cm

Answer 1

分析 根据圆周角定理求出∠AOD，求出∠OAD，根据含30度角的直角三角形性质和勾股定理求出AD、OD，根据垂径定理即可求出AB．

解答 解：∵∠CBA=30°，
∴∠AOC=2∠CBA=60°，
∵AB⊥OC，
∴∠ADO=90°，
∴∠OAD=30°，
∴OD=$\frac{1}{2}$OA=$\frac{1}{2}$×2=1（cm），
由勾股定理得：AD=$\sqrt{O{A}^{2}-O{D}^{2}}$=$\sqrt{3}$cm，
∵AB⊥OC，OC过O，
∴AB=2AD=2$\sqrt{3}$（cm），
故选B．

点评 本题考查了垂径定理，含30度角的直角三角形性质，圆周角定理，勾股定理的应用，主要考查学生的推理和计算能力．