题目内容
9．多项式6m3-2m2+4m+2减去3（2m3+m2+3m-1），再减去3（2m3+m2+3m-1）（m为整数）的差一定是（ ）| A． | 5的倍数 | B． | 偶数 | C． | 3的倍数 | D． | 不能确定 |
分析 先把6m3-2m2+4m+2-3（2m3+m2+3m-1）-3（2m3+m2+3m-1）去括号，合并同类项，得到-6m3-8m2-14m+8，即化简的结果为2（-3m3-4m2-7m+4），于是可判断差为2的倍数．
解答 解：6m3-2m2+4m+2-3（2m3+m2+3m-1）-3（2m3+m2+3m-1）
=6m3-2m2+4m+2-6m3-3m2-9m+3-6m3-3m2-9m+3
=-6m3-8m2-14m+8
=2（-3m3-4m2-7m+4）
因为m为整数，显然差为2的倍数，即为偶数．
故选B．
点评 本题考查了整式的加减：几个整式相加减，通常用括号把每一个整式括起来，再用加减号连接；然后去括号、合并同类项．整式的加减实质上就是合并同类项．
练习册系列答案
阅读快车系列答案
相关题目
4．
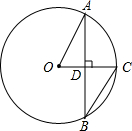如图，⊙O的弦AB垂直半径OC于点D，∠CBA=30°，OC=2cm，则弦AB的长为（ ）
如图，⊙O的弦AB垂直半径OC于点D，∠CBA=30°，OC=2cm，则弦AB的长为（ ）| A． | 9cm | B． | 2$\sqrt{3}$cm | C． | $\frac{9}{2}$ cm | D． | $\frac{3\sqrt{3}}{2}$ cm |
14．下列计算正确的是（ ）
| A． | a5-a3=a2 | B． | （-a5）2=a10 | C． | a5•a3=a15 | D． | $\frac{{a}^{6}}{{a}^{3}}$=a2 |
1．下列说法正确的是（ ）
| A． | 若|a|=-a，则a＜0 | B． | 式子3xy2-4x3y+12是七次三项式 | ||
| C． | 若a＜0，ab＜0，则b＞0 | D． | 若a=b，m是有理数，则$\frac{a}{m}$=$\frac{b}{m}$ |
19．若m，n为任意实数，则下列各式成立的是（ ）
| A． | $\sqrt{（m+n）^{2}}$=m+n | B． | $\sqrt{{m}^{2}}$+$\sqrt{{n}^{2}}$=m+n | C． | $\sqrt{mn}$=$\sqrt{m}+\sqrt{n}$ | D． | $\sqrt{（m+n）^{4}}=（m+n）^{2}$ |