题目内容
11.有六张正面分别标有数字-2、-$\frac{1}{2}$、0、1、2、3的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上,洗匀后从中任取一张,将该卡片的数字a记为点P的横坐标,将a2记为点P的纵坐标,已知P(a,a2)落在直线y=-x+n上的概率为$\frac{1}{3}$,则n的值为2.分析 根据概率公式可得直线y=-x+n上的点P(a,a2)有2个,再根据一次函数图象上点的坐标特征得出n=x+y=a+a2=2.
解答 解:∵有六张正面分别标有数字-2、-$\frac{1}{2}$、0、1、2、3的不透明卡片,
∴P(a,a2)一共有6种情况,
当a=-2、-$\frac{1}{2}$、0、1、2、3时,
a2=4、$\frac{1}{4}$、0、1、4、9,
∴a+a2=2、-$\frac{1}{4}$、0、2、6、12,
∵P(a,a2)落在直线y=-x+n上的概率为$\frac{1}{3}$,而n=y+x,
∴直线y=-x+n上的点P(a,a2)有2个,此时a+a2=2=n,
故答案为2.
点评 本题考查了概率公式,用到的知识点为:概率=所求情况数与总情况数之比.也考查了一次函数图象上点的坐标特征.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
12.设a-b+ab=0,其中ab≠0.则$\frac{1}{a}$-$\frac{1}{b}$等于( )
| A. | 1 | B. | -1 | C. | $\frac{1}{ab}$ | D. | $\frac{1}{a-b}$ |
19.下列运算中,正确的是( )
| A. | 2a+3b=5ab | B. | 3x2÷2x=x | C. | (x2)3=x6 | D. | (x+y2)2=x2+y4 |
6. 如图,在△ABC中,AB=AC,过点A作AD∥BC,若∠1=65°,则∠BAC的大小为( )
如图,在△ABC中,AB=AC,过点A作AD∥BC,若∠1=65°,则∠BAC的大小为( )
 如图,在△ABC中,AB=AC,过点A作AD∥BC,若∠1=65°,则∠BAC的大小为( )
如图,在△ABC中,AB=AC,过点A作AD∥BC,若∠1=65°,则∠BAC的大小为( )| A. | 45° | B. | 50° | C. | 60° | D. | 65° |
16.下列实数中是无理数的是( )
| A. | $\sqrt{3}$ | B. | 0 | C. | -1 | D. | $\sqrt{9}$ |
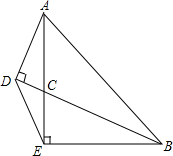 如图,△ABE中,∠AEB=90°,AE=BE,BC平分∠ABE交AE于C,AD⊥BC于D,连DE.
如图,△ABE中,∠AEB=90°,AE=BE,BC平分∠ABE交AE于C,AD⊥BC于D,连DE.