题目内容
13.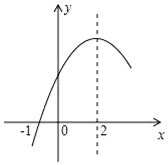 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a-3b+c>0;(3)4a+2b>m(am+b),(m≠2的实数)(4)若方程a(x+1)(x-5)=-3的两根为x1和x2,且x1<x2,则x1<-1<5<x2.其中正确的结论有( )个.
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a-3b+c>0;(3)4a+2b>m(am+b),(m≠2的实数)(4)若方程a(x+1)(x-5)=-3的两根为x1和x2,且x1<x2,则x1<-1<5<x2.其中正确的结论有( )个.| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据对称轴可判断(1),根据当x=-3时y<0可判断(2),根据函数的最值可判断(3),利用二次函数与二次方程关系可判断(4).
解答 解:∵抛物线的对称轴为直线x=-$\frac{b}{2a}$=2,
∴b=-4a>0,即4a+b=0,所以(1)正确;
∵x=-3时,y<0,
∴9a-3b+c<0,即9a+c<3b,所以(2)错误;
由图象知,当x=2时y取得最大值,最大值y=4a+2b+c,
∵m≠2的实数,
∴当x=m时,y=am2+bm+c<4a+2b+c,即4a+2b>m(am+b),所以(3)正确;
∵抛物线的对称轴为直线x=-$\frac{b}{2a}$=2,图象与x轴交于(-1,0),
∴抛物线x轴的另一个交点是(5,0),
则抛物线y=ax2+bx+c=a(x+1)(x-5),
如图所示: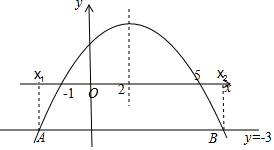
方程a(x+1)(x-5)=-3的两根可看做抛物线y=a(x+1)(x-5)与直线y=-3交点的横坐标,
由图象可知x1<-1<5<x2,所以(4)正确;
故选:B.
点评 本题主要考查二次函数图象与系数的关系,掌握①二次项系数a决定抛物线的开口方向和大小,②一次项系数b和二次项系数a共同决定对称轴的位置,③常数项c决定抛物线与y轴交点,④抛物线与x轴交点个数是解题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
5.小张文具店每月一次性购进100件文具进行销售(能全部售出),有A,B两种文具可供选择,已知A型文具的进价是每件10元,B型文具的进价是每件15元,小张发现,所获总利润y(元)与A型文具的进货量x(件)之间存在着如下表所示的一次函数关系:
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)在小张文具店中,B型文具的售价是23元;
(3)若在六月份,小张只有1300元,在进货量(100件)不变的前提下,六月份的最大利润是多少?
| 购进A型文具x件 | … | 10 | 20 | 30 | 40 | 50 | … |
| 总利润y元 | … | 740 | 680 | 620 | 560 | 500 | … |
(2)在小张文具店中,B型文具的售价是23元;
(3)若在六月份,小张只有1300元,在进货量(100件)不变的前提下,六月份的最大利润是多少?
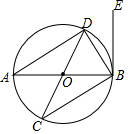 如图,在⊙O中,AB,CD是直径,BE是切线,B为切点,连接AD,BC,BD.
如图,在⊙O中,AB,CD是直径,BE是切线,B为切点,连接AD,BC,BD. 概念理解:
概念理解: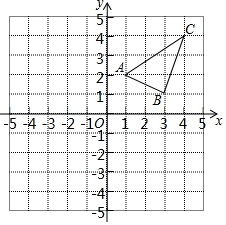 学习完轴对称后,黑板展示区出了一道作图题(不写作法,保留作图痕迹).
学习完轴对称后,黑板展示区出了一道作图题(不写作法,保留作图痕迹).