题目内容
10.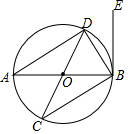 如图,在⊙O中,AB,CD是直径,BE是切线,B为切点,连接AD,BC,BD.
如图,在⊙O中,AB,CD是直径,BE是切线,B为切点,连接AD,BC,BD.(1)求证:△ABD≌△CDB;
(2)若∠DCB=37°,求∠EBD的度数.
分析 (1)根据AB,CD是直径,可得出∠ADB=∠CBD=90°,再根据HL定理得出Rt△ABD≌Rt△CDB;
(2)由BE是切线,得AB⊥BE,根据∠DCB=37°,得∠A=∠DBE=37°.
解答 (1)证明:∵AB,CD是直径,
∴∠ADB=∠CBD=90°,
在Rt△ABD和Rt△CDB中,
$\left\{\begin{array}{l}{AB=CD}\\{BD=DB}\end{array}\right.$,
∴Rt△ABD≌Rt△CDB(HL);
(2)解:∵BE是切线,
∴AB⊥BE,
∴∠ABE=90°,
∴∠DBE+∠ABD=90°
∵∠ADB=90°
∴∠A+∠ABD=90°
∴∠A=∠DBE
∵∠DCB=37°,
∴∠A=37°
∴∠DBE=37°,
∴∠DBE的度数为37°.
点评 本题考查了切线的性质以及全等三角形的判定和性质,是基础题,难度不大.

练习册系列答案
相关题目
1.方程x2+17=8x的根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 有一个实数根 | D. | 没有实数根 |
14.下列计算中,正确的是( )
| A. | a3+a3=a6 | B. | a2•a5=a7 | C. | (2a)3=2a3 | D. | 3a8÷a2=3a4 |
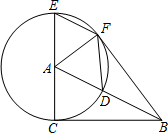 如图,已知⊙A的半径为4,EC是圆的直径,点B是⊙A的切线CB上的一个动点,连接AB交⊙A于点D,弦EF平行于AB,连接DF,AF.
如图,已知⊙A的半径为4,EC是圆的直径,点B是⊙A的切线CB上的一个动点,连接AB交⊙A于点D,弦EF平行于AB,连接DF,AF. 如图,射线OA的方向是西南方向,射线OB的方向是北偏西70°,则∠AOB=65°.
如图,射线OA的方向是西南方向,射线OB的方向是北偏西70°,则∠AOB=65°.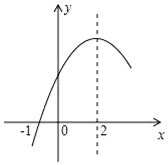 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a-3b+c>0;(3)4a+2b>m(am+b),(m≠2的实数)(4)若方程a(x+1)(x-5)=-3的两根为x1和x2,且x1<x2,则x1<-1<5<x2.其中正确的结论有( )个.
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a-3b+c>0;(3)4a+2b>m(am+b),(m≠2的实数)(4)若方程a(x+1)(x-5)=-3的两根为x1和x2,且x1<x2,则x1<-1<5<x2.其中正确的结论有( )个.