题目内容
3.在△ABC中,∠B=45°,AB=3$\sqrt{6}$,AC=6,则BC=3$\sqrt{3}±3$.分析 首先根据正弦定理即可求得∠B的正弦值,然后分∠C是锐角和钝角两种情况进行讨论即可求解.
解答 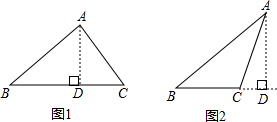 解:如图1,
解:如图1,
∵∠B=45°,AB=3$\sqrt{6}$,
∴AD=AB•sin45°=3$\sqrt{6}$×$\frac{\sqrt{2}}{2}$=3$\sqrt{3}$,
∴BD=3$\sqrt{3}$,
∵AC=6,
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{36-27}$=3,
∴BC=3$\sqrt{3}$+3;
如图2,BC=3$\sqrt{3}$-3,
∴BC=3$\sqrt{3}$±3,
故答案为:3$\sqrt{3}±3$.
点评 此题主要考查了正弦定义,以及特殊角的三角函数,正确注意到分两种情况讨论是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.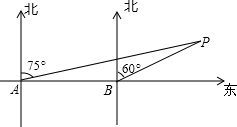 某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,继续航行7海里后,在B处测得小岛P的方位是北偏东60°,则此时轮船与小岛P的距离BP=( )
某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,继续航行7海里后,在B处测得小岛P的方位是北偏东60°,则此时轮船与小岛P的距离BP=( )
 某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,继续航行7海里后,在B处测得小岛P的方位是北偏东60°,则此时轮船与小岛P的距离BP=( )
某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,继续航行7海里后,在B处测得小岛P的方位是北偏东60°,则此时轮船与小岛P的距离BP=( )| A. | 7海里 | B. | 14海里 | C. | 3.5海里 | D. | 4海里 |
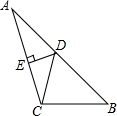 已知:△ABC中,D是AB中点,DE⊥AC于E,∠B=45°,tan∠A=$\frac{1}{2}$.
已知:△ABC中,D是AB中点,DE⊥AC于E,∠B=45°,tan∠A=$\frac{1}{2}$.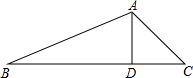 如图,AD⊥BC于D,BD=AC+DC,若∠BAC=120°,那么∠C的度数为40°.
如图,AD⊥BC于D,BD=AC+DC,若∠BAC=120°,那么∠C的度数为40°.