题目内容
18.计算题:(1)-2-5;
(2)5÷(-$\frac{3}{5}$)×$\frac{5}{3}$;
(3)(1-$\frac{1}{6}$+$\frac{3}{4}$)×(-48);
(4)-12+[20+(-2)3]÷4.
分析 (1)根据有理数减法的运算方法,求出算式的值是多少即可.
(2)首先计算除法,然后计算乘法,求出算式的值是多少即可.
(3)应用乘法分配律,求出算式的值是多少即可.
(4)首先计算乘方和括号里面的运算,然后计算除法和加法,求出算式的值是多少即可.
解答 解:(1)-2-5=-7
(2)5÷(-$\frac{3}{5}$)×$\frac{5}{3}$
=(-$\frac{25}{3}$)×$\frac{5}{3}$
=-$\frac{125}{9}$
(3)(1-$\frac{1}{6}$+$\frac{3}{4}$)×(-48)
=1×(-48)-$\frac{1}{6}$×(-48)+$\frac{3}{4}$×(-48)
=-48+8-36
=-76
(4)-12+[20+(-2)3]÷4
=-1+(20-8)÷4
=-1+12÷4
=-1+3
=2
点评 此题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.

练习册系列答案
相关题目
9.若3am+2b与ab2n-1是同类项,则m+n的值是( )
| A. | -1 | B. | -5 | C. | 2 | D. | 0 |
13.外心在三角形的一边上的三角形形状一定为( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 等腰三角形 |
3.已知a是整数,关于q的二次三项式2q2-aq-6能在有理数范围内因式分解,则a的取值有( )种.
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
8.已知等腰三角形的周长为12,一边长为5,则它的腰长等于( )
| A. | 5 | B. | 2或5 | C. | 3.5 | D. | 5或3.5 |
 如图,∠A=50°,∠BDC=70°,DE∥BC,交AB于点E,BD是△ABC的角平分线.求∠DEB的度数.
如图,∠A=50°,∠BDC=70°,DE∥BC,交AB于点E,BD是△ABC的角平分线.求∠DEB的度数. 如图,四边形ABCD的对角线相交于O点,AD=BC,作AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,且DE=BF,则下列结论:
如图,四边形ABCD的对角线相交于O点,AD=BC,作AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,且DE=BF,则下列结论: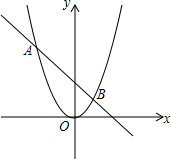 如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-4,8),B(2,2),则关于x的方程ax2-bx-c=0的解为x1=-4,x2=2.
如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-4,8),B(2,2),则关于x的方程ax2-bx-c=0的解为x1=-4,x2=2.