题目内容
8. 如图,∠A=50°,∠BDC=70°,DE∥BC,交AB于点E,BD是△ABC的角平分线.求∠DEB的度数.
如图,∠A=50°,∠BDC=70°,DE∥BC,交AB于点E,BD是△ABC的角平分线.求∠DEB的度数.
分析 根据三角形的一个外角等于与它不相邻的两个内角的和求出∠DBE,再根据角平分线的定义求出∠ABC,然后根据两直线平行,同旁内角互补求解即可.
解答 解:∵∠A=50°,∠BDC=70°,
∴∠DBE=∠BDC-∠A=70°-50°=20°,
∵BD是△ABC的角平分线,
∴∠ABC=2∠DBE=2×20°=40°,
∵DE∥BC,
∴∠DEB=180°-∠ABC=180°-40°=140°.
点评 本题考查了平行线的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,熟记性质并准确识图理清图中各角度之间的关系是解题的关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
18.下列二次根式中,能与$\sqrt{3}$合并的是( )
| A. | $\sqrt{18}$ | B. | $\sqrt{48}$ | C. | $\sqrt{6}$ | D. | $\sqrt{32}$ |
20.下列图形既是中心对称图形又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
17.下列命题中是真命题的是( )
| A. | 线段垂直平分线上的点到这条线段的两个端点的距离相等 | |
| B. | 有两边及一角相等的两个三角形全等 | |
| C. | 一个图形和经过它旋转所得的图形中,对应的所连的线段平行且相等 | |
| D. | 对角线相等的四边形是平行四边形 |
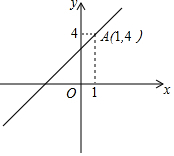 已知,一次函数y=kx+3的图象经过点A(1,4).
已知,一次函数y=kx+3的图象经过点A(1,4).