题目内容
19.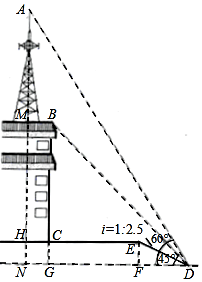 如图,某校少年宫数学课外活动初三小组的同学为测量一座铁塔AM的高度如图,他们在坡度是i=1:2.5的斜坡DE的D处,测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°,斜坡高EF=2米,CE=13米,CH=2米.大家根据所学知识很快计算出了铁塔高AM.亲爱的同学们,相信你也能计算出铁塔AM的高度!请你写出解答过程.(数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73供选用,结果保留整数)
如图,某校少年宫数学课外活动初三小组的同学为测量一座铁塔AM的高度如图,他们在坡度是i=1:2.5的斜坡DE的D处,测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°,斜坡高EF=2米,CE=13米,CH=2米.大家根据所学知识很快计算出了铁塔高AM.亲爱的同学们,相信你也能计算出铁塔AM的高度!请你写出解答过程.(数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73供选用,结果保留整数)
分析 先根据DE的坡度i=1:2.5求出FD与EF的长,进而可得出GD的长,在Rt△DBG中,由等腰直角三角形的性质得出BG=GD,在Rt△DAN中,根据∠NAD=60°,ND=NG+GD=CH+GD可得出AN的长,再由AM=AN-MN=AN-BG可得出结论.
解答 解:∵斜坡的坡度是i=$\frac{EF}{FD}$═$\frac{1}{2.5}$,EF=2,
∴FD=2.5 EF=2.5×2=5,
∵CE=13,CE=GF,
∴GD=GF+FD=CE+FD=13+5=18.
在Rt△DBG中,
∵∠GDB=45°,
∴BG=GD=18,
在Rt△DAN中,
∵∠NAD=60°,ND=NG+GD=CH+GD=2+18=20,
∴AN=ND•tan60°=20×$\sqrt{3}$=20$\sqrt{3}$,
∴AM=AN-MN=AN-BG=20$\sqrt{3}$-18≈17(米).
答:铁塔高AC约17米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,熟记锐角三角函数的定义是解答此题的关键.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
7.下列计算中,正确的是( )
| A. | 2a+3a=5a | B. | a3•a2=a6 | C. | a3÷a2=1 | D. | (-a)3=a3 |
 (1)计算:$\frac{5}{\sqrt{5}}$-(2-$\sqrt{5}$)0+($\frac{1}{2}$)-2
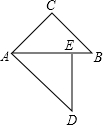
(1)计算:$\frac{5}{\sqrt{5}}$-(2-$\sqrt{5}$)0+($\frac{1}{2}$)-2 如图,△ABC中,AB=7,AC=5,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为1.
如图,△ABC中,AB=7,AC=5,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为1.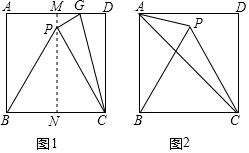 取一张正方形的纸片进行折叠,具体操作过程如下:
取一张正方形的纸片进行折叠,具体操作过程如下: