题目内容
10. 如图,△ABC中,AB=7,AC=5,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为1.
如图,△ABC中,AB=7,AC=5,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为1.
分析 首先证明△AGF≌△ACF,则AG=AC=5,GF=CF,证明EF是△BCG的中位线,利用三角形的中位线定理即可求解.
解答 解:在△AGF和△ACF中,
$\left\{\begin{array}{l}{∠GAF=∠CAF}\\{AF=AF}\\{∠AFG=∠AFC}\end{array}\right.$,
∴△AGF≌△ACF,
∴AG=AC=5,GF=CF,
则BG=AB-AG=7-5=2.
又∵BE=CE,
∴EF是△BCG的中位线,
∴EF=$\frac{1}{2}$BG=1.
故答案为1.
点评 本题考查了全等三角形的判定以及三角形的中位线定理,正确证明GF=CF是关键.

练习册系列答案
相关题目
20.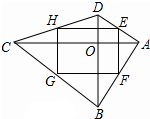 在四边形ABCD中,对角线AC与BD交于点O,点E、F、G、H分别为边AD,AB,BC,CD的中点,则四边形EFGH为矩形,则需要添加的条件是( )
在四边形ABCD中,对角线AC与BD交于点O,点E、F、G、H分别为边AD,AB,BC,CD的中点,则四边形EFGH为矩形,则需要添加的条件是( )
 在四边形ABCD中,对角线AC与BD交于点O,点E、F、G、H分别为边AD,AB,BC,CD的中点,则四边形EFGH为矩形,则需要添加的条件是( )
在四边形ABCD中,对角线AC与BD交于点O,点E、F、G、H分别为边AD,AB,BC,CD的中点,则四边形EFGH为矩形,则需要添加的条件是( )| A. | AC平分BD | B. | AC⊥BD | C. | AC=BD | D. | AC与BD互相平分 |
5.化简:($\sqrt{x-3}$)2=( )
| A. | x-3 | B. | 3-x | C. | x+3 | D. | ±(x-3) |

 如图,△A1B1C1是边长为1的等边三角形,A2为等边△A1B1C1的中心,连接A2B1并延长到点B2,使A2B1=B1B2,以A2B2为边作等边△A2B2C2,A3为等边△A2B2C2的中心,连接A3B2并延长到点B3,使A3B2=B2B3,以A3B3为边作等边△A3B3C3,依次作下去得到等边△AnBnCn,则等边△A6B6C6的边长为$\frac{32\sqrt{3}}{27}$.
如图,△A1B1C1是边长为1的等边三角形,A2为等边△A1B1C1的中心,连接A2B1并延长到点B2,使A2B1=B1B2,以A2B2为边作等边△A2B2C2,A3为等边△A2B2C2的中心,连接A3B2并延长到点B3,使A3B2=B2B3,以A3B3为边作等边△A3B3C3,依次作下去得到等边△AnBnCn,则等边△A6B6C6的边长为$\frac{32\sqrt{3}}{27}$.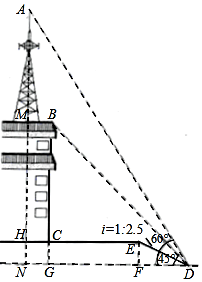 如图,某校少年宫数学课外活动初三小组的同学为测量一座铁塔AM的高度如图,他们在坡度是i=1:2.5的斜坡DE的D处,测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°,斜坡高EF=2米,CE=13米,CH=2米.大家根据所学知识很快计算出了铁塔高AM.亲爱的同学们,相信你也能计算出铁塔AM的高度!请你写出解答过程.(数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73供选用,结果保留整数)
如图,某校少年宫数学课外活动初三小组的同学为测量一座铁塔AM的高度如图,他们在坡度是i=1:2.5的斜坡DE的D处,测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°,斜坡高EF=2米,CE=13米,CH=2米.大家根据所学知识很快计算出了铁塔高AM.亲爱的同学们,相信你也能计算出铁塔AM的高度!请你写出解答过程.(数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73供选用,结果保留整数)