题目内容
13．
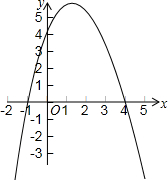已知二次函数y=-x2+3x+4的图象．（1）方程-x2+3x+4=0的解是-1或4．
（2）不等式-x2+3x+4＞0的解集是-1＜x＜4；
（3）不等式-x2+3x+4＜0的解集是x＞4或x＜-1．
分析 （1）由函数的图象可知：抛物线和x轴交点的横坐标为-1和4，进而可得方程-x2+3x+4=0的解；
（2）结合函数的图形可知图象在x轴上方时对应的x取值范围是-1＜x＜4，进而可得不等式-x2+3x+4＞0的解集；
（3）结合函数的图形可知图象在x轴下方时对应的x取值范围是x＞4或x＜-1，进而可得不等式-x2+3x+4＞0的解集．
解答 解：（1）∵抛物线y=-x2+3x+4和x轴交点的横坐标为-1和4，
∴对应方程-x2+3x+4=0的解为-1或4，
故答案为：-1或4；
（2）由函数的图形可知图象在x轴上方时对应的x取值范围是-1＜x＜4，所以不等式-x2+3x+4＞0的解集为-1＜x＜4，
故答案为：-1＜x＜4；
（3）由函数的图形可知图象在x轴下方时对应的x取值范围是x＞4或x＜-1，所以不等式-x2+3x+4＞0的解集为x＞4或x＜-1，
故答案为：x＞4或x＜-1．
点评 本题考查了二次函数与不等式，抛物线与x轴的交点，此类题目主要利用数形结合的思想求解．
练习册系列答案
相关题目
3．在实数0，-$\sqrt{3}$，1，-2中最小的是（ ）
| A． | -2 | B． | -$\sqrt{3}$ | C． | 0 | D． | 1 |
已知，如图，把长方形纸片ABCD沿EF折叠后，点D与点B重合，点C落在点C′的位置上，若∠1=60°，AE=2．
5．下列计算错误的是（ ）
| A． | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B． | $\sqrt{2}•\sqrt{3}=\sqrt{6}$ | C． | ${（\sqrt{3}）^2}=3$ | D． | $（\sqrt{3}+\sqrt{2}）（\sqrt{3}-\sqrt{2}）=1$ |
2．下列几何体中，不属于多面体的是（ ）
| A． | 六棱柱 | B． | 直三棱柱 | C． | 长方体 | D． | 圆柱 |