题目内容
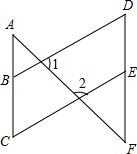已知，如图∠1=52°，∠2=128°，∠C=∠D．探索∠A与∠F的数量关系，并说明理由．请你认真完成下面的填空．解：∠A=∠F
理由如下：
∵∠1=52°，∠2=128°（已知）
∴∠1+∠2=180°
∴BD∥CE
∴∠C=
∵∠C=∠D（已知）
∴∠D=
∴AC∥DF
∴
考点：平行线的判定与性质
专题：推理填空题
分析：根据平行线的判定方法和性质分别填空即可．
解答：解：∵∠1=52°，∠2=128°（已知）
∴∠1+∠2=180°
∴BD∥CE（同旁内角互补，两直线平行）
∴∠C=∠ABD（两直线平行，同位角相等）
∵∠C=∠D（已知）
∴∠D=∠ABD（等量代换）
∴AC∥DF（内错角相等，两直线平行）
∴∠A=∠F（两直线平行，内错角相等）．
故答案为：（同旁内角互补，两直线平行），∠ABD（两直线平行，同位角相等），∠ABD（等量代换），（内错角相等，两直线平行），∠A=∠F（两直线平行，内错角相等）．
∴∠1+∠2=180°
∴BD∥CE（同旁内角互补，两直线平行）
∴∠C=∠ABD（两直线平行，同位角相等）
∵∠C=∠D（已知）
∴∠D=∠ABD（等量代换）
∴AC∥DF（内错角相等，两直线平行）
∴∠A=∠F（两直线平行，内错角相等）．
故答案为：（同旁内角互补，两直线平行），∠ABD（两直线平行，同位角相等），∠ABD（等量代换），（内错角相等，两直线平行），∠A=∠F（两直线平行，内错角相等）．
点评：本题考查了平行线的判定与性质，主要是逻辑思维能力的训练，熟记平行线的判定方法和性质是解题的关键．
练习册系列答案
相关题目
在平面直角坐标系中，点P（6，-5）在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
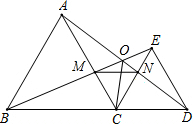如图，已知△ABC和△CDE均是等边三角形，点B、C、D在同一条直线上，BE与AD交于点O，AD与CE交于点N，AC与BE交于点M，连接OC、MN，则下列结论：