题目内容
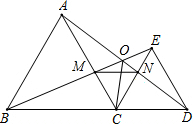 如图,已知△ABC和△CDE均是等边三角形,点B、C、D在同一条直线上,BE与AD交于点O,AD与CE交于点N,AC与BE交于点M,连接OC、MN,则下列结论:
如图,已知△ABC和△CDE均是等边三角形,点B、C、D在同一条直线上,BE与AD交于点O,AD与CE交于点N,AC与BE交于点M,连接OC、MN,则下列结论:①AD=BE;②AN=BM;③MN∥BD;④∠BOC=∠DOC,⑤△CMN为等边三角形,⑥若∠ADE=20°,则∠BED=100°,
其中正确的结论个数为( )
| A、3个 | B、4个 | C、5个 | D、6个 |
考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:根据等边三角形的性质可得AC=BC,CD=CE,∠ACB=∠DCE,再求出∠ACD=∠BCE,然后利用“边角边”证明△ACD和△BCE全等,根据全等三角形对应边相等可得AD=BE,判断出①正确,全等三角形对应角相等可得∠ADC=∠BEC,∠CAD=∠CBE,再求出∠ACN=∠BCM=60°,然后利用“边角边”证明△ACN和△BCM全等,根据全等三角形对应边相等可得AN=BM,CM=CN,判断出②正确,根据全等三角形对应角相等可得∠BOC=∠ACN=60°,再求出∠DOC=60°,从而得到∠BOC=∠DOC,判断出④正确;判断出△CMN为等边三角形,判断出⑤正确,根据等边三角形的性质可得∠CMN=60°,得到∠ACB=∠CMN,再根据内错角相等,两直线平行可得MN∥BD,判断出③正确;求出∠ADC,即为∠BEC,再根据∠BED=∠BEC+∠CED计算即可得解,从而判断出⑥正确.
解答:解:∵△ABC和△CDE均是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE,
∴∠ACB+∠ACE=∠DCE+∠ACE,
即∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,(故①正确);
∠ADC=∠BEC,∠CAD=∠CBE,
∵∠ACN=180°-2×60°=60°,
∴∠ACN=∠BCM=60°,
在△ACN和△BCM中,
,
∴△ACN≌△BCM(ASA),
∴AN=BM,CM=CN,(故②正确);
∠BOC=∠ACN=60°,
∵∠CBE+∠ADC=∠CBE+∠BEC=∠DCE=60°,
∴∠BOD=180°-(∠CBE+∠ADC)=180°-60°=120°,
∴∠DOC=∠BOD-∠BOC=120°-60°=60°,
∴∠BOC=∠DOC,(故④正确);
∵∠ACN=60°,CM=CN,
∴△CMN为等边三角形,(故⑤正确);
∴∠CMN=60°,
∴∠ACB=∠CMN=60°,
∴MN∥BD,(故③正确);
∵∠ADE=20°,
∴∠ADC=∠CDE-∠ADE=60°-20°=40°,
∴∠BEC=40°,
∴∠BED=∠BEC+∠CED=40°+60°=100°,(故⑥正确);
综上所述,结论正确的是①②③④⑤⑥共6个.
故选:D.
∴AC=BC,CD=CE,∠ACB=∠DCE,
∴∠ACB+∠ACE=∠DCE+∠ACE,
即∠ACD=∠BCE,
在△ACD和△BCE中,
|
∴△ACD≌△BCE(SAS),
∴AD=BE,(故①正确);
∠ADC=∠BEC,∠CAD=∠CBE,
∵∠ACN=180°-2×60°=60°,
∴∠ACN=∠BCM=60°,
在△ACN和△BCM中,
|
∴△ACN≌△BCM(ASA),
∴AN=BM,CM=CN,(故②正确);
∠BOC=∠ACN=60°,
∵∠CBE+∠ADC=∠CBE+∠BEC=∠DCE=60°,
∴∠BOD=180°-(∠CBE+∠ADC)=180°-60°=120°,
∴∠DOC=∠BOD-∠BOC=120°-60°=60°,
∴∠BOC=∠DOC,(故④正确);
∵∠ACN=60°,CM=CN,
∴△CMN为等边三角形,(故⑤正确);
∴∠CMN=60°,
∴∠ACB=∠CMN=60°,
∴MN∥BD,(故③正确);
∵∠ADE=20°,
∴∠ADC=∠CDE-∠ADE=60°-20°=40°,
∴∠BEC=40°,
∴∠BED=∠BEC+∠CED=40°+60°=100°,(故⑥正确);
综上所述,结论正确的是①②③④⑤⑥共6个.
故选:D.
点评:本题考查了全等三角形的判定与性质,等边三角形的性质与判定,熟练掌握各性质与判定方法是解题的关键,难点在于需要多次证明三角形全等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
点M(-2,1)在第( )象限.
| A、一 | B、二 | C、三 | D、四 |
 如图,菱形ABCD中,∠B=60°,以AC为边长的正方形ACEF的面积为3,则菱形ABCD的面积为( )
如图,菱形ABCD中,∠B=60°,以AC为边长的正方形ACEF的面积为3,则菱形ABCD的面积为( )| A、3 | ||||
B、
| ||||
C、3
| ||||
D、
|
已知点P(2,-1),则点P位于平面直角坐标系中的( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
关于x的一元二次方程(k-2)2x2+(2k+1)x+1=0有两个不相等的实数根,则k的取值范围是( )
A、k>
| ||
B、k≥
| ||
C、k≥
| ||
D、k>
|
如图中是对顶角的是( )
A、 |
B、 |
C、 |
D、 |
 如图,直角△ABC中,∠A=90°,∠B=30°,AC=4,以A为圆心,AC长为半径画四分之一圆,则图中阴影部分的面积是
如图,直角△ABC中,∠A=90°,∠B=30°,AC=4,以A为圆心,AC长为半径画四分之一圆,则图中阴影部分的面积是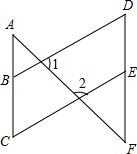 已知,如图∠1=52°,∠2=128°,∠C=∠D.探索∠A与∠F的数量关系,并说明理由.请你认真完成下面的填空.
已知,如图∠1=52°,∠2=128°,∠C=∠D.探索∠A与∠F的数量关系,并说明理由.请你认真完成下面的填空.