题目内容
某工厂要加工m个零件,甲队单独完成需n小时,乙队单独完成比甲队少用0.5小时,则两队一起加工这批零件需要多少小时?
考点:列代数式(分式)
专题:
分析:我们把这批零件看做单位“1”,甲队的工作效率是
,乙队的工作效率是
,两队合作的工作效率是
+
,用工作量单位“1”除以这个工作效率是他们的工作时间.
| 1 |
| n |
| 1 |
| n-0.5 |
| 1 |
| n |
| 1 |
| n-0.5 |
解答:解:∵甲队的工作效率是
,乙队的工作效率是
,
∴两队合作的工作效率是
+
=
+
=
+
=-
=
,
1÷
=n(1-2n).
答:两队一起加工这批零件需要n(1-2n)小时.
| 1 |
| n |
| 1 |
| n-0.5 |
∴两队合作的工作效率是
| 1 |
| n |
| 1 |
| n-0.5 |
| 1 |
| n |
| 1 | ||
n-
|
| 1 |
| n |
| 2 |
| 2n-1 |
| 1 |
| n(2n-1) |
| 1 |
| n(1-2n) |
1÷
| 1 |
| n(1-2n) |
答:两队一起加工这批零件需要n(1-2n)小时.
点评:本题考查了列代数式,求出甲乙两队的工作效率是解决此题的关键.

练习册系列答案
相关题目
月球的质量约为73400 000 000亿吨,用科学记数法表示这个数是( )
| A、734×108亿吨 |
| B、73.4×109亿吨 |
| C、7.34×1010亿吨 |
| D、0.734×1011亿吨 |
下列关于邻补角的说法,正确的是( )
| A、和为180°的两个角互为邻补角 |
| B、有公共顶点且互补的两个角互为邻补角 |
| C、有一条公共边且有一条公共边,另一边互为反向延长线的两个角互为邻补角 |
| D、有公共顶点且有一条公共边,另一边互为反向延长线的两个角互为邻补角 |
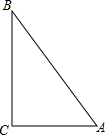 如图,点A表示小雨家,点B表示小樱家,点C表示小丽家,她们三家恰好组成一个直角三角形,其中AC⊥BC,AC=900米,BC=1200米,AB=1500米.
如图,点A表示小雨家,点B表示小樱家,点C表示小丽家,她们三家恰好组成一个直角三角形,其中AC⊥BC,AC=900米,BC=1200米,AB=1500米.
 P为等边△ABC内一点,PA=5,PB=4,PC=3,求∠BPC.
P为等边△ABC内一点,PA=5,PB=4,PC=3,求∠BPC.