题目内容
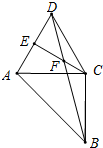 如图,以等腰直角△ABC的直角边AC作等边△ACD,CE⊥AD于E,BD、CE交于点F.
如图,以等腰直角△ABC的直角边AC作等边△ACD,CE⊥AD于E,BD、CE交于点F.(1)求∠DFE的度数;
(2)求证:AB=2DF.
考点:等腰直角三角形,等边三角形的判定与性质
专题:
分析:(1)根据等边三角形的性质可得∠ACD的大小,根据BC=CD即可求得∠CDB,即可求得∠ADB,即可解题;
(2)根据∠DFE=45°可得△DEF为等腰直角三角形,根据AD=2DE即可解题.
(2)根据∠DFE=45°可得△DEF为等腰直角三角形,根据AD=2DE即可解题.
解答:解:(1)∵△ACD是等边三角形,
∴∠ACD=60°,
∴∠BCD=60°+90°=150°,
∵BC=CD
∴∠BDC=
(180°-150°)=15°,
∴∠ADE=60°-15°=45°,
∴∠DFE=180°-∠DEF-∠EDF=45°,
(2)∵CE⊥AD,∠DFE=45°,
∴△DEF为等腰直角三角形,
∵△ABC是等腰直角三角形,
∴△ACB∽△DEF,
∴
=
=
,
∴AB=2DE.
∴∠ACD=60°,
∴∠BCD=60°+90°=150°,
∵BC=CD
∴∠BDC=
| 1 |
| 2 |
∴∠ADE=60°-15°=45°,
∴∠DFE=180°-∠DEF-∠EDF=45°,
(2)∵CE⊥AD,∠DFE=45°,
∴△DEF为等腰直角三角形,
∵△ABC是等腰直角三角形,
∴△ACB∽△DEF,
∴
| DE |
| AC |
| DF |
| AB |
| 1 |
| 2 |
∴AB=2DE.
点评:本题考查了三角形内角和为180°的性质,考查了三角形相似的判定和相似三角形对应边比例相等的性质,本题中求证△DEF是等腰直角三角形解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,在O点的观测站测得渔船A、B的方向分别为北偏东45°,南偏西30°,为了减少相互干扰并取得较好的捕鱼效益,渔船C恰好位于∠AOB的平分线上,求渔船C相对观测站的方向.
如图所示,在O点的观测站测得渔船A、B的方向分别为北偏东45°,南偏西30°,为了减少相互干扰并取得较好的捕鱼效益,渔船C恰好位于∠AOB的平分线上,求渔船C相对观测站的方向. P为等边△ABC内一点,PA=5,PB=4,PC=3,求∠BPC.
P为等边△ABC内一点,PA=5,PB=4,PC=3,求∠BPC.