题目内容
 如图,正方形ABCD的对角线相交于O,点F在AD上,AD=3AF,△AOF的外接圆交AB于E,则
如图,正方形ABCD的对角线相交于O,点F在AD上,AD=3AF,△AOF的外接圆交AB于E,则| AE |
| AF |
A、
| ||
| B、3 | ||
C、
| ||
| D、2 |
考点:三角形的外接圆与外心,正方形的性质
专题:计算题
分析:连结OE、OF,作OH⊥AD于H,OP⊥AB于E,如图,设AF=x,则AD=3x,根据正方形的性质得∠OAF=∠OAE=45°,切可判断四边形APOH为正方形,则OF=OE,AP=OP=OH=AH=
x,FH=AH-AF=
x,再根据“HL”可判断Rt△OFH≌Rt△OEP,得到FH=PE=
x,所以AE=AP+PE=2x,然后计算
的值.
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| AE |
| AF |
解答:解:连结OE、OF,作OH⊥AD于H,OP⊥AB于E,如图,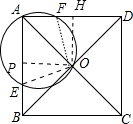 设AF=x,则AD=3x,
设AF=x,则AD=3x,
∵正方形ABCD的对角线相交于O,
∴∠OAF=∠OAE=45°,四边形APOH为正方形,
∴OF=OE,AP=OP=OH=AH=
x,
∴FH=AH-AF=
x-x=
x,
在Rt△OFH和Rt△OEP中,
,
∴Rt△OFH≌Rt△OEP(HL),
∴FH=PE=
x,
∴AE=AP+PE=
x+
x=2x,
∴
=
=2.
故选D.
 设AF=x,则AD=3x,
设AF=x,则AD=3x,∵正方形ABCD的对角线相交于O,
∴∠OAF=∠OAE=45°,四边形APOH为正方形,
∴OF=OE,AP=OP=OH=AH=
| 3 |
| 2 |
∴FH=AH-AF=
| 3 |
| 2 |
| 1 |
| 2 |
在Rt△OFH和Rt△OEP中,
|
∴Rt△OFH≌Rt△OEP(HL),
∴FH=PE=
| 1 |
| 2 |
∴AE=AP+PE=
| 3 |
| 2 |
| 1 |
| 2 |
∴
| AE |
| AF |
| 2x |
| x |
故选D.
点评:本题考查了三角形的外接圆与外心:经过三角形的三个顶点的圆,叫做三角形的外接圆.三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.也考查了直角三角形的全等的判定与性质和正方形的性质.

练习册系列答案
相关题目
 如图,∠1的同位角是
如图,∠1的同位角是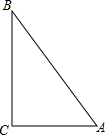 如图,点A表示小雨家,点B表示小樱家,点C表示小丽家,她们三家恰好组成一个直角三角形,其中AC⊥BC,AC=900米,BC=1200米,AB=1500米.
如图,点A表示小雨家,点B表示小樱家,点C表示小丽家,她们三家恰好组成一个直角三角形,其中AC⊥BC,AC=900米,BC=1200米,AB=1500米.
 P为等边△ABC内一点,PA=5,PB=4,PC=3,求∠BPC.
P为等边△ABC内一点,PA=5,PB=4,PC=3,求∠BPC.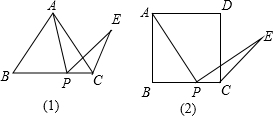 (1)在正△ABC中,P在BC上,∠APE=∠B,PE与∠C的外角平分线交于E,求证:AP=PE.
(1)在正△ABC中,P在BC上,∠APE=∠B,PE与∠C的外角平分线交于E,求证:AP=PE.