题目内容
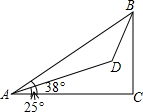某勘测队在山脚测得山顶的仰角为38°，沿倾斜角为25°的山坡前进800米后，又测得山顶的仰角为62°，求山的高度（精确到0.1米）．（cos13°=0.9744，sin13°=0.2250，cot24°=2.246，sin38°=0.6157）．考点：解直角三角形的应用-仰角俯角问题
专题：
分析：首先根据题意分析图形；作DE⊥AB于E构造两个直角三角形，分别求解可得AE与EB的值，再利用图形关系，进而可求出答案．
解答：解：作DE⊥AB于E，
∵AD=800，
∴AE=AD•cos∠EAD=AD•cos13°，
DE=AD•sin∠EAD=AD•sin13°，
∵BE•cot∠ABD=ED，
∴BE=
=
，
AB=AE+BE=AD•cos13°+
=859.66米，
∴BC=AB•sin38°=529.3米．
∵AD=800，
∴AE=AD•cos∠EAD=AD•cos13°，
DE=AD•sin∠EAD=AD•sin13°，
∵BE•cot∠ABD=ED，
∴BE=
| DE |
| cot∠ABD |
| DE |
| cot24° |
AB=AE+BE=AD•cos13°+
| AD•sin13° |
| cot24° |
∴BC=AB•sin38°=529.3米．
点评：本题考查了直角三角形中三角函数的运用，本题中求AE，BE的值是解题的关键．
练习册系列答案
相关题目
如图，△ABC以AB为直径，中点O为圆心作圆交BC于P，使BP=CP，作PE⊥AC，求证：PE为切线．（用两种方法）
P为等边△ABC内一点，PA=5，PB=4，PC=3，求∠BPC．