下列图形中.既是中心对称.又是轴对称图形的是( )A．B．C．D．题目和参考答案——青夏教育精英家教网—

题目内容

8．下列图形中，既是中心对称，又是轴对称图形的是（　　）

A．

B．

C．

D．

分析根据中心对称图形与轴对称图形的概念，即：把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形；如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形．结合选项解答即可．

解答解：A、是轴对称图形，也是中心对称图形；
B、是轴对称图形，不是中心对称图形；
C、不是轴对称图形，不是中心对称图形；
D、不是轴对称图形，是中心对称图形．
故选A．

点评本题考查了中心对称图形与轴对称图形的知识，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合；中心对称图形的关键是要寻找对称中心，旋转180度后两部分重合．

练习册系列答案

相关题目

18．

如图，在正方形ABCD内有一点P满足AP=AB，PB=PC，连接AC、PD．求证：△APB≌△DPC．

19．

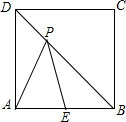如图，P是边长为1的正方形ABCD的对角线BD上的一点，点E是AB的中点，则PA+PE的最小值是（　　）

$\frac{1}{2}$$+\frac{\sqrt{2}}{2}$

D．

$\sqrt{2}$

16．

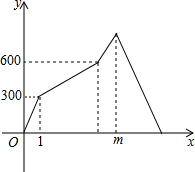老王乘坐7：00的高铁从A地去B地开会，出发后发现一份重要的文件未带，让同事小李乘坐8：00的动车将文件送至B地．因火车会车原因，动车在途中停留了半小时．若高铁与动车的行驶路线相同、行驶过程中两车都以各自的速度匀速行驶，且A地到B地的全线长为1350千米．设高铁出发时间为t小时，高铁与动车的距离为y千米，y与t的函数图象如图所示．（注：高铁出发时，动车在A地；高铁到达B地后进行补给，直至动车到达B地．）
（1）高铁速度为300km/h，m=4.5h．
（2）求动车的速度．
（3）若小李当天16：00前能到达B地火车站，老王的会议就不会受影响，请通过计算说明老王的会议会不会受影响．

$\frac{{3{x^2}}}{4xy}$

B．

$\frac{{{x^2}+{y^2}}}{x+y}$

C．

$\frac{x-2}{{{x^2}-4}}$

D．

$\frac{1+x}{{{x^2}+2x+1}}$

20．计算：|-2|+2⁰-（-1）²=（　　）

17．为了降低塑料袋--“白色污染”对环境污染．学校组织了对使用购物袋的情况的调查，小明同学5月8日到站前市场对部分购物者进行了调查，据了解该市场按塑料购物袋的承重能力分别提供了0.1元，0.2元，0.3元三种质量不同的塑料袋，下面两幅图是这次调查得到的不完整的统计图（若每人每次只使用一个购物袋），请你根据图中的信息，回答下列问题：
（1）这次调查的购物者总人数是120人；
（2）请补全条形统计图，并说明扇形统计图中0.2元部分所对应的圆心角是99度，0.3元部分所对应的圆心角是36度；
（3）若5月8日到该市场购物的人数有3000人次，则该市场应销售塑料购物袋多少个？

a⁴•a²=a⁸

b³+b³=b⁶

x⁶÷x²=x³

（y²）⁴=y⁸

试题分类