Question

19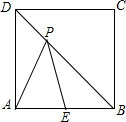．如图，P是边长为1的正方形ABCD的对角线BD上的一点，点E是AB的中点，则PA+PE的最小值是（　　）

• A． $\frac{\sqrt{5}}{2}$
• B． $\frac{\sqrt{6}}{2}$
• C． $\frac{1}{2}$$+\frac{\sqrt{2}}{2}$
• D． $\sqrt{2}$

Answer 1

分析 利用轴对称最短路径求法，得出A点关于BD的对称点为C点，再利用连接EC交BD于点P即为最短路径位置，利用勾股定理求出即可．

解答 解：连接AC，EC，EC与BD交于点P，此时PA+PE的最小，
∵正方形ABCD中，AB=BC=1，E为AB中点，
∴BE=$\frac{1}{2}$，
∴EC=$\sqrt{B{C}^{2}+B{E}^{2}}$=$\frac{\sqrt{5}}{2}$，
故选A．

点评 此题主要考查了利用轴对称求最短路径问题以及正方形的性质和勾股定理，利用正方形性质得出A，C关于BD对称是解题关键．