题目内容
10.按照某一规律排列的一组数据,它的前五个数是:1,$\frac{3}{4}$,$\frac{5}{9}$,$\frac{7}{16}$,$\frac{9}{25}$,按照这样的规律,这组数据的第10项应该是$\frac{19}{100}$.分析 设该组数列中第n个数为an(n为正整数),根据给定数据列出部分an的值,根据数的变换找出变换规律“an=$\frac{2n-1}{{n}^{2}}$”,依此变换规律即可得出结论.
解答 解:设该组数列中第n个数为an(n为正整数),
观察,发现规律:a1=1=$\frac{1}{1}$,a2=$\frac{3}{4}$=$\frac{3}{{2}^{2}}$,a3=$\frac{5}{9}$=$\frac{5}{{3}^{2}}$,a4=$\frac{7}{16}$=$\frac{7}{{4}^{2}}$,a5=$\frac{9}{25}$=$\frac{9}{{5}^{2}}$,…,
∴an=$\frac{2n-1}{{n}^{2}}$.
∴a10=$\frac{2×10-1}{1{0}^{2}}$=$\frac{19}{100}$.
故答案为:$\frac{19}{100}$.
点评 本题考查了规律型中的数字的变化类,解题的关键是找出变换规律an=$\frac{2n-1}{{n}^{2}}$.本题属于基础题,难度不大,解决该题型题目时,列出该数列中前几个数,根据数的变化找出变化规律是关键.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
2.要使分式$\frac{-5}{x-1}$有意义,则x的取值范围是( )
| A. | x≠1 | B. | x>1 | C. | x<1 | D. | x≠-1 |
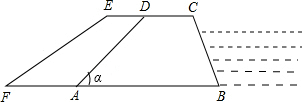 如图,某堤坝的横截面是梯形ABCD,背水坡AD的坡度(即tanα)为1:1.2,坝高10米,为了提高坝的防洪能力,由相关部门决定加固堤坝,要求将坝顶CD加宽2米,形成新的背水坡EF,其坡度为1:1.4,已知堤坝总长度为1000米.
如图,某堤坝的横截面是梯形ABCD,背水坡AD的坡度(即tanα)为1:1.2,坝高10米,为了提高坝的防洪能力,由相关部门决定加固堤坝,要求将坝顶CD加宽2米,形成新的背水坡EF,其坡度为1:1.4,已知堤坝总长度为1000米.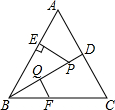 如图,△ABC是等边三角形,P是∠ABC的平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC于点F,垂足为点Q.如果BF=a,那么PE=$\frac{\sqrt{3}}{2}$a(用含a的代数式表示).
如图,△ABC是等边三角形,P是∠ABC的平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC于点F,垂足为点Q.如果BF=a,那么PE=$\frac{\sqrt{3}}{2}$a(用含a的代数式表示). 如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面约4米高,球落地后又一次弹起,据试验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面约4米高,球落地后又一次弹起,据试验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半. 如图,在平面直角坐标系xOy中,点m在x轴的正半轴上,⊙M交x轴于A、B两点,交y轴于C,D两点,且C为弧AE的中点,AE交y轴于G点,若点A的坐标为(-2,0),AE=8,
如图,在平面直角坐标系xOy中,点m在x轴的正半轴上,⊙M交x轴于A、B两点,交y轴于C,D两点,且C为弧AE的中点,AE交y轴于G点,若点A的坐标为(-2,0),AE=8,