题目内容
12.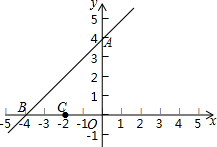 如图,已知直线l的解析式为y=x+4与y轴交于A点,与x轴交于B点.
如图,已知直线l的解析式为y=x+4与y轴交于A点,与x轴交于B点.(1)写出A、B两点的坐标;
(2)又知点C(-2,0),请在直线l上找一点P,使得OP+CP的值最小,求P点的坐标.
分析 (1)把x=0,y=0代入解答即可;
(2)根据轴对称的性质解答即可.
解答 解:(1)把x=0代入y=x+4=4,点A的坐标为(0,4);
把y=0代入y=x+4,解得:x=-4,点B的坐标为(-4,0),
(2)点O关于l的轴对称点O'(-4,4),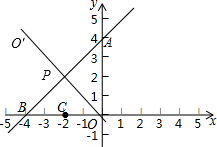
连接O'C交l于点P,
则OP+CP=O'P+CP=O'C=$\sqrt{{2}^{2}+{4}^{2}}=2\sqrt{5}$为最小,
设经过O'、C两点的直线解析式为y=mx+n,
将O'(-4,4),(-2,0)分别代入,
得$\left\{\begin{array}{l}{4=-4m+n}\\{0=-2m+n}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=-2}\\{n=-4}\end{array}\right.$,
所以经过O'、C两点的直线解析式为y=-2x-4,
联立$\left\{\begin{array}{l}{y=x+4}\\{y=-2x-4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=-\frac{8}{3}}\\{y=\frac{4}{3}}\end{array}\right.$.
所以点P的坐标为($-\frac{8}{3}$,$\frac{4}{3}$).
点评 本题考查了轴对称的问题,关键是根据直线的交点坐标解答.

练习册系列答案
相关题目
 完成下列推理填空:
完成下列推理填空: