题目内容
2．图1、图2是两张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点，在每张方格纸中均画有线段AB，点A、B均在格点上．（1）在图1中画一个以AB为斜边的等腰直角三角形ABC，使点C在AB右侧的格点上；
（2）在图2中画一个以AB为对角线且面积为40的菱形ADBE，使点D、E均在格点，并直接写出菱形ADBE的边长．
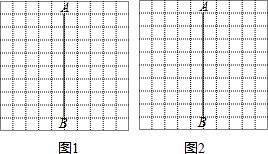
分析 （1）根据AB为斜边的等腰直角三角形ABC可知直角顶点C在AB的中垂线上，且在直线AB右侧格点上，找到一点即可；
（2）根据菱形性质可知对角线互相垂直且平分，可知点D、E在AB的中垂线上，根据AB=8、菱形面积为80可得DE=10，确定即可，根据勾股定理求得边长．
解答 解：（1）如图1，
（2）如图2，菱形边长为$\sqrt{{4}^{2}+{5}^{2}}$=$\sqrt{41}$．
点评 本题主要考查勾股定理、等腰直角三角形及菱形的性质，剖析两个图形的特点，根据条件逐步确定顶点的位置是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
12．
如果，正方形ABCD的边长为2cm，E为CD边上一点，∠DAE=30°，M为AE的中点，过点M作直线分别与AD、BC相交于点P、Q，若PQ=AE，则PD等于（ ）
如果，正方形ABCD的边长为2cm，E为CD边上一点，∠DAE=30°，M为AE的中点，过点M作直线分别与AD、BC相交于点P、Q，若PQ=AE，则PD等于（ ）| A． | $\frac{2}{3}$cm或$\frac{2}{3}\sqrt{3}$cm | B． | $\frac{2}{3}\sqrt{3}$cm | C． | $\frac{4}{3}$cm或$\frac{2}{3}\sqrt{3}$cm | D． | $\frac{2}{3}$cm或$\frac{4}{3}$cm |
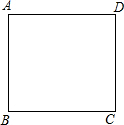如图是一张边长为3cm的正方形纸片ABCD．现要利用这张正方形纸片剪出一个腰长为2cm的等腰三角形，要求等腰三角形的一个顶点与正方形的一个顶点重合，另外两个顶点都在正方形的边上，则剪下的等腰三角形的面积为2或$\sqrt{3}$cm2．
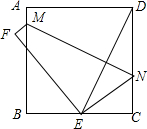将一张边长为4cm的正方形纸片沿MN对折，使点D落在BC边上．
如图，AB是⊙O的直径，过点B作BC⊥AB，过点A作AD∥OC交⊙O于点D，连结BD．若AB=6，BC=4，求AD的长．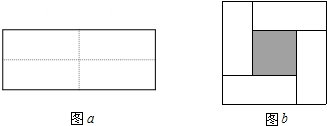
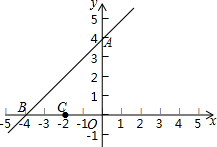如图，已知直线l的解析式为y=x+4与y轴交于A点，与x轴交于B点．