题目内容
17.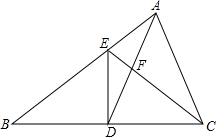 如图,在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.
如图,在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.(1)△ABC与△FCD相似吗?请说明理由.
(2)点F是线段AD的中点吗?为什么?
(3)若S△ABC=20,BC=10,求DE的长.
分析 (1)由线段垂直平分线的性质可知BE=EC,从而可知∠ABC=∠FCD,然后由AD=AC可知∠ACB=∠FDC,从而可证明△ABC与△FCD相似;
(2)由相似三角形的性质可知DF:AC=1:2,由AC=AD,从而得到DF=$\frac{1}{2}AD$;
(3)过点A作AG⊥BC,由三角形的面积公式求得AG的长,然后根据△BED相似△BAG求解即可.
解答 解:(1)∵D是BC的中点,DE⊥BC,
∴BE=EC.
∴∠ABC=∠FCD.
∵AD=AC,
∴∠ACB=∠FDC.
∴△ABC∽△FCD.
(2)∵△ABC∽△FCD,
∴$\frac{DF}{AC}=\frac{DC}{BC}$=$\frac{1}{2}$.
∴DF=$\frac{1}{2}AC$.
∵AD=AC,
∴$DF=\frac{1}{2}AD$.
∴点F是AD的中点.
(3)过点A作AG⊥BC,垂足为G.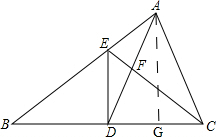
∵S△ABC=20,BC=10,
∴AG=4.
∵D是BC的中点,
∴DB=DC=5.
∵AD=AC,AG⊥DC,
∴DG=DC=2.5.
∵ED⊥BC,AG⊥BC,
∴DE∥AG.
∴$\frac{DE}{AG}=\frac{BD}{BG}$,即$\frac{DE}{4}=\frac{2}{3}$.
解得:DE=$\frac{8}{3}$.
点评 本题主要考查的是相似三角形的性质和判定,掌握相似三角形的性质和判定定理是解题的关键.

练习册系列答案
相关题目
 如图所示,已知△ABC≌△DEF,AB=AC=DE=DF,E是BC的中点,△DEF绕E旋转,求∠NME和∠CME的关系.
如图所示,已知△ABC≌△DEF,AB=AC=DE=DF,E是BC的中点,△DEF绕E旋转,求∠NME和∠CME的关系. 如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,计算点O到AB与CD边的距离之比.
如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,计算点O到AB与CD边的距离之比.