题目内容
12．
如图，在平行四边形ABCD中，E是AB的中点，CE和BD交于点O，计算点O到AB与CD边的距离之比．
分析 由四边形ABCD是平行四边形，得到AB∥CD，AB=CD，推出△OCD∽△OEB，根据相似三角形的性质得到OE：OC=1：2，即可得到结论．
解答 解：∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD，
∴△OCD∽△OEB，
∵E是AB的中点，
∴BE=$\frac{1}{2}$AB=$\frac{1}{2}$CD，
∴OE：OC=1：2，
∴点O到AB与CD边的距离之比=$\frac{1}{2}$．
点评 本题考查了相似三角形的判定和性质，平行四边形的性质，熟练掌握相似三角形的判定和性质是解题的关键．
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
18．两个互为相反数的数，它们的奇数次幂（ ）
| A． | 相等 | B． | 互为负倒数 | ||
| C． | 互为倒数 | D． | 相等或互为相反数 |
已知：如图，AB=AD，BD平分∠ABC，求证：AD∥BC．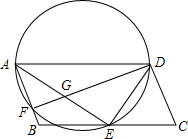
如图，在平行四边形ABCD中，E为BC边上的一点，且AE与DE分别平分∠BAD和∠ADC
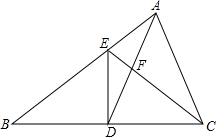如图，在△ABC中，D是BC的中点，且AD=AC，DE⊥BC，DE与AB相交于点E，EC与AD相交于点F．
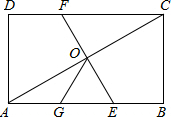如图，在矩形ABCD中，O为AC的中点，EF过O点且EF⊥AC分别交DC于E，交AB于E，点G是AE的中点，且∠AOG=30°，则下列结论：（1）DC=3OG；（2）OG=$\frac{1}{2}$BC；（3）四边形AECF为菱形；（4）S△AOE=$\frac{1}{6}$S四边形ABCD．其中正确的个数为（ ）
如图，AP为⊙O的切线，P为切点，OA交⊙O于点B．若∠A=40°，则∠ABP=115°．