题目内容
5. 如图所示,已知△ABC≌△DEF,AB=AC=DE=DF,E是BC的中点,△DEF绕E旋转,求∠NME和∠CME的关系.
如图所示,已知△ABC≌△DEF,AB=AC=DE=DF,E是BC的中点,△DEF绕E旋转,求∠NME和∠CME的关系.
分析 根据已知条件得到∠B=∠3=∠C=∠F,由三角形的内角和和平角的定义得到∠2=∠4,推出△BEN∽△CME,得到$\frac{CM}{BE}=\frac{ME}{EN}$,等量代换得到$\frac{CM}{CE}=\frac{EM}{EN}$,于是推出△CME∽△MEN,根据相似三角形的性质即可得到结论.
解答  解:∵△ABC≌△DEF,AB=AC=DE=DF,
解:∵△ABC≌△DEF,AB=AC=DE=DF,
∴∠B=∠3=∠C=∠F,
∴∠1+∠2=180°-∠3,∠1+∠4=180°-∠B,
∴∠2=∠4,
∴△BEN∽△CME,
∴$\frac{CM}{BE}=\frac{ME}{EN}$,
∵BE=CE,
∴$\frac{CM}{CE}=\frac{EM}{EN}$,
∴△CME∽△MEN,
∴∠NME=∠CME.
点评 本题考查了相似三角形的判定和性质,全等三角形的性质,等腰三角形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
14.用配方法解一元二次方程x2-6x+4=0,下列变形正确的是( )
| A. | (x-3)2=13 | B. | (x-3)2=5 | C. | (x-6)2=13 | D. | (x-6)2=5 |
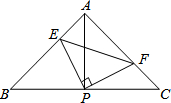 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论: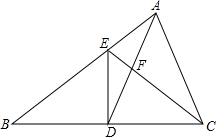 如图,在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.
如图,在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F. 如图,在△ABC中,D是BC边的中点,AE:DE=1:3,若S${\;}_{△ABC}=16c{m}^{2}$,则S△ABE=2cm2.
如图,在△ABC中,D是BC边的中点,AE:DE=1:3,若S${\;}_{△ABC}=16c{m}^{2}$,则S△ABE=2cm2.