题目内容
5.已知函数y=(m+1)x${\;}^{{m}^{2}-3m-2}$+(m-1)x(m是常数).m为何值时,它是一次函数?分析 直接利用一次函数的定义进而分析得出答案.
解答 解:∵一次函数y=(m+1)x${\;}^{{m}^{2}-3m-2}$+(m-1)x(m是常数),
∴m2-3m-2=1,
解得:m=$\frac{3±\sqrt{21}}{2}$,
当m+1=0,
解得:m=-1,
综上所述:m=$\frac{3±\sqrt{21}}{2}$或-1时,它是一次函数.
点评 此题主要考查了一次函数的定义,正确把握一次函数的系数与次数的关系是解题关键.

练习册系列答案
相关题目
15.如果m>n,那么下列不等式中成立的是( )
| A. | 1-m<1-n | B. | 2m<2n | C. | -m>-n | D. | 1+m<1+n. |
16.下列各式中正确的是( )
| A. | -2a3•3a2=-6a5 | B. | 3a2•4a2=12a2 | C. | (a+1)(a-1)=a2-a+1 | D. | a15÷a3=a5(a≠0) |
13.下列运算正确的是( )
| A. | (a-b)(a+c)=a2-ab+ac+bc | B. | x2•x3=x6 | ||
| C. | (x-2)2=x2-42 | D. | 5-1=$\frac{1}{5}$ |
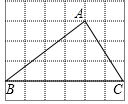 如图,网格图中的每个小正方形的边长都是1,△ABC每个顶点都在格点上,则cosB=$\frac{4}{5}$.
如图,网格图中的每个小正方形的边长都是1,△ABC每个顶点都在格点上,则cosB=$\frac{4}{5}$.