Question

8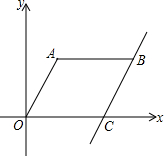．如图，已知点C坐标为（6，0），将线段OC向右平移3个单位，再向上平移4个单位得到线段AB，连接OA，此时OA=5．
（1）求四边形OABC的面积；
（2）过点A作AD⊥x轴，垂足为点D，P是从O出发以每秒1个单位的速度向x轴正方向运动，Q是直线BC上一点，当△PCQ与△OAD全等时，求t的值．

Answer 1

分析 （1）根据线段OC平移，可得四边形OABC是平行四边形，根据平行四边形面积公式，可得答案；
（2）分类讨论：①△CQ₁P₁≌△OAD，②△CQ₂P₂≌△OAD，③△P₃Q₃C≌△ADO，④△P₄Q₄C≌△ADO，根据全等三角形的性质，可得CP的长，根据线段的和差，可得答案．

解答 解：（1）如图1作AD⊥OC于D，
由点C坐标为（6，0），将线段OC向右平移3个单位，再向上平移4个单位得到线段AB，得
A坐标（3，4）B坐标（9，4），D（3，0）．
S_{四边形OABC}=OC•AD=6×4=24；
（2）如图2，
①当△CQ₁P₁≌△OAD时，CP₁=OD=3，OP=3，即t=3秒；
②当△CQ₂P₂≌△OAD时，CP₂=OD=3，OP₂=OC+CP₂=6+3=9，即t=9秒；
如图3，
③当△P₃Q₃C≌△ADO时，P₃C=OA=5，OP₃=OC-CP₃=6-5=1，即t=1秒；
④当△P₄Q₄C≌△ADO时，CP₄=OA=5，OP₄=OC+CP₄=6+5=11，即t=11秒；
综上所述：t=3秒，t=9秒，t=1秒，t=11秒．

点评 本题考查了一次函数综合题，（1）利用线段平移得出平行四边形是解题关键；（2）利用全等三角形的性质得出CP的长是解题关键，要分类讨论，以防遗漏．